Cho tam giác ABC vuông cân tại A. Gọi M là trung điểm của BC. Lấy điểm D trên đoạn thẳng AB, đường thẳng vuông góc với MD tại M cắt AC tại E. Cmr:MD=ME.b) trên tia đối của tia CA lấy điểm K sao cho CK=BD, ĐK cắt BC tại I. Cmr:I là trung điểm của DK.c) đường vuông góc với ĐK tại I cắt AM tại S. Cmr: SC vuông góc với AK.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$ac=b^2\Rightarrow \frac{a}{b}=\frac{b}{c}$
$bd=c^2\Rightarrow \frac{b}{c}=\frac{c}{d}$
$\Rightarrow \frac{a}{b}=\frac{b}{c}=\frac{c}{d}$
Đặt $\frac{a}{b}=\frac{b}{c}=\frac{c}{d}=k\Rightarrow a=bk; b=ck; c=dk$
Khi đó:
$\frac{a}{d}=\frac{bk}{d}=\frac{ck^2}{d}=\frac{dk^3}{d}=k^3(1)$
Lại có:
$(\frac{2a+3b-c}{2b+3c-d})^3=(\frac{2bk+3b-c}{2ck+3c-d})^3=(\frac{2ck^2+3ck-c}{2dk^2+3dk-d})^3$
$=[\frac{c(2k^2+3k-1)}{d(2k^2+3k-1)}]^3=(\frac{c}{d})^3=(\frac{dk}{d})^3=k^3(2)$
Từ $(1); (2)$ ta có đpcm.

\(\dfrac{1}{1\cdot3}+\dfrac{1}{3\cdot5}+...+\dfrac{1}{2021\cdot2023}\)
\(=\dfrac{1}{2}\left(\dfrac{2}{1\cdot3}+\dfrac{2}{3\cdot5}+...+\dfrac{2}{2021\cdot2023}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...+\dfrac{1}{2021}-\dfrac{1}{2023}\right)\)
\(=\dfrac{1}{2}\left(1-\dfrac{1}{2023}\right)=\dfrac{1}{2}\cdot\dfrac{2022}{2023}=\dfrac{1011}{2023}\)
=1/1.3+1/3.5+1/5.7+......+1/2021.2023
=1/1-1/3+1/3-1/5+....+1/2021-1/2023
=1/1-1/2023
=1-1/2023
=2023/2023-1/2023
=2022/2023
Đáp án là : 2022/2023
(không bít có đúng không nữa :_3)


1,8m=18dm; 0,2m=2dm; 0,4m=4dm
Thể tích khối gỗ là:
\(18\cdot2\cdot4=144\left(dm^3\right)\)
Khối lượng của khối gỗ là:
\(144\cdot0,8=115,2\left(kg\right)\)


Số mét vải cần dùng để may 1 chiếc khăn là:
4:5=0,8(mét)
May 1 chiếc khăn hết số mét vải là:
4 : 5 = 0,8 (m)
Đ/S : 0,8 m vải
:>

a: \(\dfrac{4}{13}+\dfrac{-12}{39}=\dfrac{4}{13}-\dfrac{4}{13}=0\)
b: \(\dfrac{27}{23}-\dfrac{-5}{21}-\dfrac{4}{23}+\dfrac{16}{21}+\dfrac{1}{2}\)
\(=\left(\dfrac{27}{23}-\dfrac{4}{23}\right)+\left(\dfrac{5}{21}+\dfrac{16}{21}\right)+\dfrac{1}{2}\)
\(=1+1+\dfrac{1}{2}=\dfrac{5}{2}\)
c: \(\dfrac{-8}{9}+\dfrac{1}{9}\cdot\dfrac{2}{9}+\dfrac{1}{9}\cdot\dfrac{7}{9}\)
\(=\dfrac{-8}{9}+\dfrac{1}{9}\left(\dfrac{2}{9}+\dfrac{7}{9}\right)\)
\(=\dfrac{-8}{9}+\dfrac{1}{9}=\dfrac{-7}{9}\)
d: \(\dfrac{2}{\left(-3\right)^2}+\dfrac{5}{-12}-\dfrac{-3}{4}\)
\(=\dfrac{2}{9}-\dfrac{5}{12}+\dfrac{3}{4}\)
\(=\dfrac{8}{36}-\dfrac{15}{36}+\dfrac{27}{36}=\dfrac{19}{36}\)
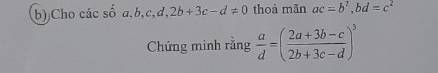
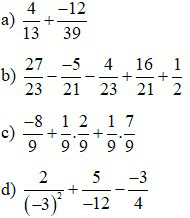
a: ΔABC vuông cân tại A
mà AM là đường trung tuyến
nên AM là phân giác của góc BAC
=>\(\widehat{BAM}=\widehat{CAM}=\dfrac{90^0}{2}=45^0\)
Xét tứ giác ADME có \(\widehat{EMD}+\widehat{EAD}=90^0+90^0=180^0\)
nên ADME là tứ giác nội tiếp
=>\(\widehat{MAD}=\widehat{MED};\widehat{MDE}=\widehat{MAE}\)
mà \(\widehat{MAD}=\widehat{MAE}=45^0\)
nên \(\widehat{MED}=\widehat{MDE}=45^0\)
=>MD=ME
b: Kẻ DF\(\perp\)AB(F\(\in\)BC)
mà AC\(\perp\)AB
nên DF//AC
DF//AC
=>\(\widehat{DFB}=\widehat{ACB}\)
mà \(\widehat{ACB}=\widehat{ABC}\)
nên \(\widehat{DFB}=\widehat{FBD}\)
=>ΔDFB cân tại D
=>DF=DB
mà DB=CK
nên DF=CK
Xét tứ giác DFKC có
DF//CK
DF=CK
Do đó: DFKC là hình bình hành
=>DK cắt FC tại trung điểm của mỗi đường
=>I là trung điểm chung của DK và FC