Giải hệ phương trình:\(\hept{\begin{cases}\sqrt{2x+1}+\sqrt{2y+1}=\frac{\left(x-y\right)^2}{2}\\\left(3x+2y\right)\left(y+1\right)=4-x^2\end{cases}}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
XO
30 tháng 12 2019
Ta có : A = 121212 x 5656
= 12 x 10101 x 56 x 101
B = 1212 x 565656 = 12 x 101 x 56 x 10101
=> A = B
30 tháng 12 2019
Bài giải:
Ta có:
\(A=121212.5656=12.10101.56.101=\left(12.101\right).\left(56.10101\right)\)\(=1212.565656=B\)
\(\Rightarrow A=B\)
Vậy: \(A=B\)
14 tháng 12 2020
Giá tiền 1kg đường năm nay so với năm trước tăng sô % là: 16000: 14400= 1,1111= 111,11% vậy số tiền năm nay mua được số kg đường là: (14400×35):16000=31,5kg
Đáp số: 31,5kg đường
CT
27 tháng 11 2021
Giá tiền 1kg đường năm nay so với năm trước tăng số phần trăm là :
16000 : 14400 = 1,1111 = 111,11%
Số tiền năm nay mua được số kg đường là :
( 14400 x 35 ) : 16000 = 31,5 kg
Đáp số : 111,11% ; 31,5kg đường
30 tháng 12 2019
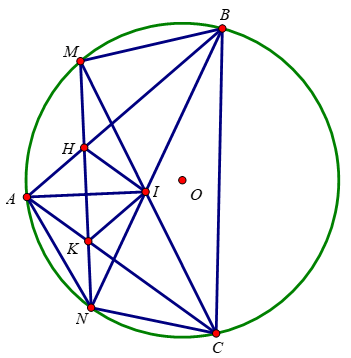
a) Xét tứ giác HMBI có:
∠HMI = ∠HBI (2 góc nội tiếp chắn 2 cung bằng nhau \(\widebat{AN}=\widebat{CN}\))
Mà 2 góc này cùng nhìn cạnh HI
=> Tứ giác BMHI nội tiếp
b) Xét ΔMNI và ΔMKC có:
∠KMC là góc chung
∠MNI = ∠KCM (2 góc nội tiếp chắn 2 cung bằng nhau \(\widebat{AM}=\widebat{BM}\))
=> ΔMNI ∼ ΔMCK => \(\frac{MN}{MC}=\frac{MI}{MK}\) => MN.MK = MC.MI
c) Xét tứ giác NKIC có:
∠KNI = ∠KCI (2 góc nội tiếp chắn 2 cung bằng nhau \(\widebat{AM}=\widebat{MB}\))
Mà 2 góc này cùng nhìn cạnh KI
=> Tứ giác NKIC là tứ giác nội tiếp
=> ∠NKI + ∠NCI = 180o (1)
Xét đường tròn (O) có:
\(\hept{\begin{cases}\widehat{ANK}=\widehat{ACM}\left(\text{2 góc nội tiếp cùng chắn cung AM}\right)\\\widehat{NAK}=\widehat{NCA}\left(\text{2 góc nội tiếp cùng chắn 2 cung BẰNG NHAU}\widebat{AN}=\widebat{CN}\right)\end{cases}}\)
=> ∠ANK + ∠NAK = ∠ACM + ∠NCA = ∠NCI (2)
Xét tam giác AKN có: ∠ANK + ∠NAK + ∠NKA = 180o (3)
Từ (1), (2), (3) => ∠NKI = ∠NKA
Xét tam giác IKN và tam giác AKN có:
∠NKI = ∠NKA
KN là cạnh chung
∠KNI = ∠KNA (2 góc nội tiếp chắn 2 cung bằng nhau)
=> ΔIKN = ΔAKN
=> IK=AK =>ΔAKI cân tại K
Tứ giác NKIC là tứ giác nội tiếp
Mặt khác ∠KCN = ∠ABN (2 góc nội tiếp cùng chắn cung AN của (O))
∠BAC = ∠BNC (2 góc nội tiếp cùng chắc cung BC của (O))
=> Tứ giác AHIK là hình bình hành
Mà IK = AK
=> Tứ giác AHIK là hình thoi.
CÒN LẠI TỰ LÀM LÀM NHA
PA
1
30 tháng 12 2019
Ta có: (x2 - 4)2 + 3 = 3 - (x - 2)2
=> [(x - 2)(x + 2)]2 + 3 - 3 + (x - 2)2 = 0
=> (x - 2)2(x + 2)2 + (x - 2)2 = 0
=> (x - 2)2[(x + 2)2 + 1] = 0
=> \(\orbr{\begin{cases}x-2=0\\\left(x+2\right)^2+1=0\end{cases}}\)
=> \(\orbr{\begin{cases}x=2\\\left(x+2\right)^2=-1\left(ktm\right)\end{cases}}\)
Vậy x = 2
30 tháng 12 2019
Chiều dài là gì v ? Mik lấy tạm là m nhé
Chiều cao của hình tam giác đó là:
4/7 x 2/5 = 8/35 (m)
Diện tích hình tam giác đó là:
(4/7 x 8/35) : 2 = 16/245 (m2)
Đ/s: ........
HN
26 tháng 4 2024
1.vì h nằm giữa IM
nên IH+HM=IM
2. vì M nằm giữa IK
nên IM + MK= IK
IM=IK-MK
từ điều 1 và 2 ta có thể suy ra rằng
2IM=(IH+HM)+(IK-MK)
2IM=IH+IK+HM-MK
mà M là trung điểm của HK
nên HM=HK
=> 2IM+IH+IK
=> IM=(IH+IK):2
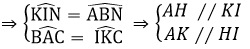
Đặt \(\sqrt{2x+1}=a,\sqrt{2y+1}=b\) thì pt thứ 2 trở thành: \(2\left(a+b\right)=\frac{\left(a^2-b^2\right)^2}{2}\)
=> 2 TH \(\orbr{\begin{cases}a+b=0\\2=\frac{\left(a-b\right)^2\left(a+b\right)}{4}\left(1\right)\end{cases}}\)
pt trên thì dễ r
pt (1) <=> \(8=\left(a-b\right)^2\left(a+b\right)=>8=\frac{\left(\sqrt{2x+1}-\sqrt{2y+1}\right)^2\left(x-y\right)^2}{2} =>16=\left(\sqrt{2x+1}-\sqrt{2y+1}\right)^2\left(x-y\right)^2\)
đến đây xét 2 Th
đặt nhìn cho dễ nhá
đặt x-y=c
khi đó ta có \(\hept{\begin{cases}\left(a-b\right)c=4\\a+b=\frac{c^2}{2}\end{cases}}\)
nhân từng vế 2 pt trên ta có a^2-b^2=2c=> 2x+2y+2=2(x-y)=> 2y+1=0...
tương tự mấy Th còn lại
\(\hept{\begin{cases}\sqrt{2x+1}+\sqrt{2y+1}=\frac{\left(x-y\right)^2}{2}\left(1\right)\\\left(x+y\right)\left(x+2y\right)+3x+2y=4\left(2\right)\end{cases}}\)
ĐK \(\hept{\begin{cases}x\ge\frac{-1}{2}\\y\ge\frac{-1}{2}\end{cases}}\)
PT (2) <=> \(x^2+\left(3y+3\right)x+2y^2+2y-4=0\Leftrightarrow\orbr{\begin{cases}x+y-1=0\\x+2y+4=0\left(loai\right)\end{cases}}\)
PT (1) <=> \(\sqrt{2x+1}-\sqrt{2y+1}=\frac{\left(x+y\right)^2-4xy}{2}\)
\(\Leftrightarrow2\left(x+y\right)+2+2\sqrt{4xy+2\left(x+y\right)+1}=\left(\frac{\left(x+y\right)^2-4xy}{2}\right)^2\)
\(\Leftrightarrow8\sqrt{4xy+3}=\left(4xy+3\right)\left(4xy-5\right)\)
\(\Leftrightarrow\orbr{\begin{cases}4xy+3=0\\\left(4xy-5\right)\sqrt{4xy+3}=8\left(loai\right)\left(1=\left(x+y\right)^2\ge4xy\Rightarrow4xy-5< 0\right)\end{cases}}\)
Hệ phương trình đã cho tương đương
\(\hept{\begin{cases}x+y=1\\xy=\frac{3}{4}\end{cases}\Leftrightarrow\hept{\begin{cases}x=\frac{1}{2}\\y=\frac{3}{2}\end{cases}}}\)và \(\hept{\begin{cases}x=\frac{3}{2}\\y=\frac{-1}{2}\end{cases}}\)
Vậy hệ phương trình đã cho có 2 nghiệm \(\left(x;y\right)=\left(\frac{-1}{2};\frac{3}{2}\right);\left(\frac{3}{2};-\frac{1}{2}\right)\)