 vẽ hình cho mik luôn nhé
vẽ hình cho mik luôn nhé
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a. Xét tam giác $MHB$ và $MKC$ có:
$\widehat{MHB}=\widehat{MKC}=90^0$
$MB=MC$ (do $M$ là trung điểm $BC$)
$\widehat{MBH}=\widehat{MCK}$ (do $ABC$ cân tại $A$)
$\Rightarrow \triangle MHB=\triangle MKC$ (ch-gn)
b.
Xét tam giác $MHA$ và $MKA$ có:
$MA$ chung
$\widehat{MHA}=\widehat{MKA}=90^0$
$MH=MK$ (hệ quả từ $\triangle MHB=\triangle MKC$ phần a)
$\Rightarrow \triangle MHA=\triangle MKA$ (ch-cgv)

y = k/x (k khác 0)
<=> x = k/y (k khác 0)
Chúc bạn học tốt nhé


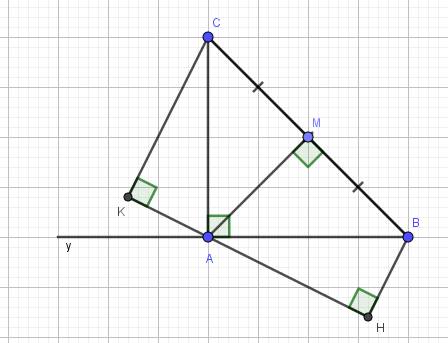
a) Xét hai tam giác vuông:\(\Delta AMB\) và \(\Delta AMC\) có:
\(BM=MC\left(gt\right)\)
AM là cạnh chung
\(\Rightarrow\Delta AMB=\Delta AMC\) (hai cạnh góc vuông)
\(\Rightarrow AB=AC\) (hai cạnh tương ứng)
b) Vẽ tia đối của tia AB là tia Ay
Ta có:
\(AB\perp AC\) (\(\Delta ABC\) vuông tại A)
\(\Rightarrow AC\perp Ay\)
\(\Rightarrow\widehat{yAK}+\widehat{KAC}=90^0\)
Lại có:
\(\widehat{yAK}=\widehat{BAH}\) (đối đỉnh)
\(\Rightarrow\widehat{BAH}+\widehat{KAC}=90^0\)
Mà \(\widehat{ACK}+\widehat{KAC}=90^0\) (\(\Delta ACK\) vuông tại K)
\(\Rightarrow\widehat{BAH}=\widehat{ACK}\)
Do \(\Delta AMB=\Delta AMC\left(cmt\right)\)
\(\Rightarrow AB=AC\) (hai cạnh tương ứng)
Xét hai tam giác vuông: \(\Delta AHB\) và \(\Delta CKA\) có:
\(AB=AC\left(cmt\right)\)
\(\widehat{BAH}=\widehat{ACK}\left(cmt\right)\)
\(\Rightarrow\Delta AHB=\Delta CKA\) (cạnh huyền - góc nhọn)

Lời giải:
Xét tam giác $ABD$ và $AED$ có:
$AB=AE$ (gt)
$\widehat{BAD}=\widehat{EAD}$ (do $AD$ là tia phân giác $\widehat{A}$)
$AD$ chung
$\Rightarrow \triangle ABD=\triangle AED$ (c.g.c)
$\Rightarrow BD=ED$ (đpcm)

Lời giải:
Vì $I$ nằm trên đường trung trực của $BC$ nên $BI=CI$
Vì $I$ nằm trên đường phân giác $\widehat{BAC}$ nên khoảng cách từ $I$ đến $AB$ bằng khoảng cách từ $I$ đến $AC$
$\Rightarrow IH=IK$
Xét tam giác vuông $IHB$ và $IKC$ có:
$IH=IK$ (cmt)
$IB=IC$ (cmt)
$\Rightarrow \triangle IHB=\triangle IKC$ (ch-gn)
$\Rightarrow HB=KC$ (đpcm)
Hình vẽ: