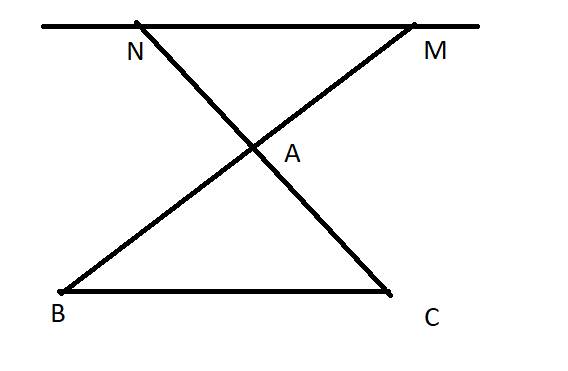
Cho tam giác ABC vuông tại A có D là trung điểm của BC. Trên AD lấy điểm M bất kì, Gọi E và F là hình chiếu của M trên AB, AC.
1) Chứng minh EF//BC
2) Kẻ EN vuông góc với FD
a)Tính góc ANM
b) Chứng minh NE là phân giác của góc ANM
3) Chứng minh 3 điểm B, M, N thẳng hàng