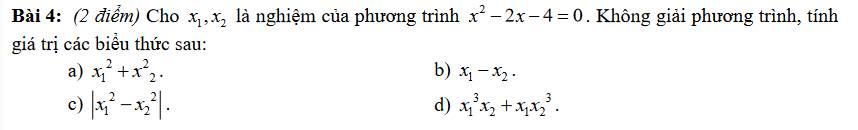Vận tốc này à bn :)

Gọi vận tốc lúc đầu của người đó là x(km/h)

(Điều kiện: x>0)

Thời gian dự kiến ban đầu là \(\dfrac{90}{x}\left(giờ\right)\)

1h9p=1,15h

Sau 1,15h, người đó đi được 1*x=x(km)

Độ dài quãng đường còn lại là 90-x(km)

Thời gian thực tế đi hết quãng đường là:

\(1,15+\dfrac{90-x}{x+4}\left(giờ\right)\)

Theo đề, ta có: 

\(\dfrac{90}{x}=1,15+\dfrac{90-x}{x+4}\)

=>\(\dfrac{90}{x}-\dfrac{90-x}{x+4}=1,15\)

=>\(\dfrac{90x+360-90x+x^2}{x\left(x+4\right)}=1,15\)

=>\(1,15\left(x^2+4x\right)=x^2+360\)

=>\(1,15x^2+4,6x-x^2-360=0\)

=>\(0,15x^2+4,6x-360=0\)

=>\(\left[{}\begin{matrix}x=36\left(nhận\right)\\x=-\dfrac{200}{3}\left(loại\right)\end{matrix}\right.\)

Vậy: Vận tốc lúc đầu của người đó là 36km/h

Gọi vận tốc của ô tô thứ nhất là x(km/h)

(Điều kiện: x>0)

vận tốc của ô tô thứ hai là x+20(km/h)

Thời gian xe ô tô thứ nhất đi từ A đến chỗ gặp là:

10h30p-6h=4h30p=4,5(giờ)

Thời gian xe ô tô thứ hai đi từ A đến chỗ gặp là:

10h30p-7h30p=3(giờ)

Độ dài quãng đường ô tô thứ nhất đi từ A đến chỗ gặp là 

4,5x(km)

Độ dài quãng đường ô tô thứ hai đi từ A đến chỗ gặp là:

3(x+20)(km)

Do đó, ta có phương trình:

4,5x=3(x+20)

=>4,5x=3x+60

=>1,5x=60

=>x=60:1,5=40(nhận)

Vậy: Vận tốc của ô tô thứ nhất là 40km/h

Vận tốc của ô tô thứ hai là 40+20=60km/h

a: Theo Vi-et, ta có:

\(x_1+x_2=-\dfrac{b}{a}=2;x_1x_2=-4\)

\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2\)

\(=2^2-2\cdot\left(-4\right)=4+8=12\)

b: \(\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2\)

\(=2^2-4\cdot\left(-4\right)=20\)

=>\(x_1-x_2=\pm2\sqrt{5}\)

c: \(\left|x_1^2-x_2^2\right|\)

\(=\left|\left(x_1-x_2\right)\left(x_1+x_2\right)\right|\)

\(=\left|2\sqrt{5}\cdot2\right|=4\sqrt{5}\)

d: \(x_1^3\cdot x_2+x_1\cdot x_2^3\)

\(=x_1x_2\left(x_1^2+x_2^2\right)\)

\(=-4\cdot12=-48\)

ủa câu này em hỏi bên dưới rồi mà?

\(x_1+x_2=-\dfrac{b}{a}=-5;x_1x_2=2\)

\(x_1^2\cdot x_2^3+x_2^2\cdot x_1^3\)

\(=\left(x_1x_2\right)^2\cdot\left(x_1+x_2\right)\)

\(=2^2\cdot\left(-5\right)=-20\)

Pt: \(x^2+5x+2=0\)

Theo vi-ét: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-5}{1}=-5\\x_1x_2=\dfrac{2}{1}=2\end{matrix}\right.\)

a) \(x^2_1+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=\left(-5\right)^2-2\cdot2=25-4=21\)

b) \(x_1^3+x_2^3=\left(x_1+x_2\right)\left(x_1^2+x_1x_2+x_2^2\right)=\left(x_1+x_2\right)\left[\left(x_1+x_2\right)^2-2x_1x_2-x_1x_2\right]\)

\(=\left(x_1+x_2\right)\left[\left(x_1+x_2\right)^2-3x_1x_2\right]=\left(-5\right)\cdot\left[\left(-5\right)^2-3\cdot2\right]=-95\)  

c) \(\left|x_1-x_2\right|=\sqrt{\left|x_1-x_2\right|^2}=\sqrt{x_1^2+x_2^2-2\left|x_1x_2\right|}\)

\(=\sqrt{\left(x_1+x_2\right)^2-2x_1x_2-2\left|x_1x_2\right|}=\sqrt{\left(-5\right)^2-2\cdot2-2\cdot\left|2\right|}=\sqrt{17}\) 

d) \(x_1^2x_2^3+x_2^2x_1^3=x_1^2x_2^2\left(x_1+x_2\right)=\left(x_1x_2\right)^2\cdot\left(x_1+x_2\right)=2^2\cdot\left(-5\right)=-20\)

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-5\\x_1x_2=2\end{matrix}\right.\)

\(x_1^2+x_2^2=\left(x_1+x_2\right)^2-2x_1x_2=\left(-5\right)^2-2.2=21\)

\(x_1^3+x_2^3=\left(x_1+x_2\right)^3-3x_1x_2\left(x_1+x_2\right)=\left(-5\right)^3-3.2.\left(-5\right)=-95\)

\(\left|x_1-x_2\right|=\sqrt{\left(x_1-x_2\right)^2}=\sqrt{\left(x_1+x_2\right)^2-4x_1x_2}=\sqrt{\left(-5\right)^2-4.2}=\sqrt{17}\)

\(x_1^2x_2^3+x_1^3x_2^2=\left(x_1x_2\right)^2\left(x_1+x_2\right)=2^2.\left(-5\right)=-20\)

là bằng 6 đó

6

Gọi thời gian đi từ A đến B là x(giờ)

(ĐK: x>0)

Thời gian đi từ B đến C là x+0,5(giờ)

Độ dài quãng đường từ A đến B là 10x(km)

Độ dài quãng đường từ B đến C là 9(x+0,5)(km)

Độ dài AC là 33km nên ta có:

10x+9(x+0,5)=33

=>19x+4,5=33

=>19x=33-4,5=30-1,5=28,5

=>x=1,5(nhận)

vậy: Thời gian đi từ A đến B là 1,5 giờ

Thời gian đi từ B đến C là 1,5+0,5=2 giờ