E= \(1^2+2^2+3^2+...+99^2+100^2\) .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


=1+ 2 (1+1)+ (2+1 )3+...+(99+1)100
=1+2+1.2+2.3+3+...+99.100+100
=(1+2+3+...+100)+(1.2+2.3+...+99.100)
=5050+(1.2+2.3+...+99.100)
đặt A=1.2+2.3+...+99.100
=>3A=1.2.3+2.3.3+...+99.100.3
=1.2.3+2.3(4-1)+...+99.100(101-98)
=1.2.3-1.2.3+2.3.4-2.3.4+...+98.99.100-98.99.100+99.100.101
=999900
=>A=333300
=>M=333300+5050=338350

Lời giải:
$B=-x(x+2)-2x+100=-x^2-4x+100$
$=104-(x^2+4x+4)=104-(x+2)^2$
Do $(x+2)^2\geq 0$ với mọi $x\in\mathbb{R}$
$\Rightarrow B=104-(x+2)^2\leq 104$
Vậy $B_{\max}=104$. Giá trị này đạt tại $x+2=0\Leftrightarrow x=-2$

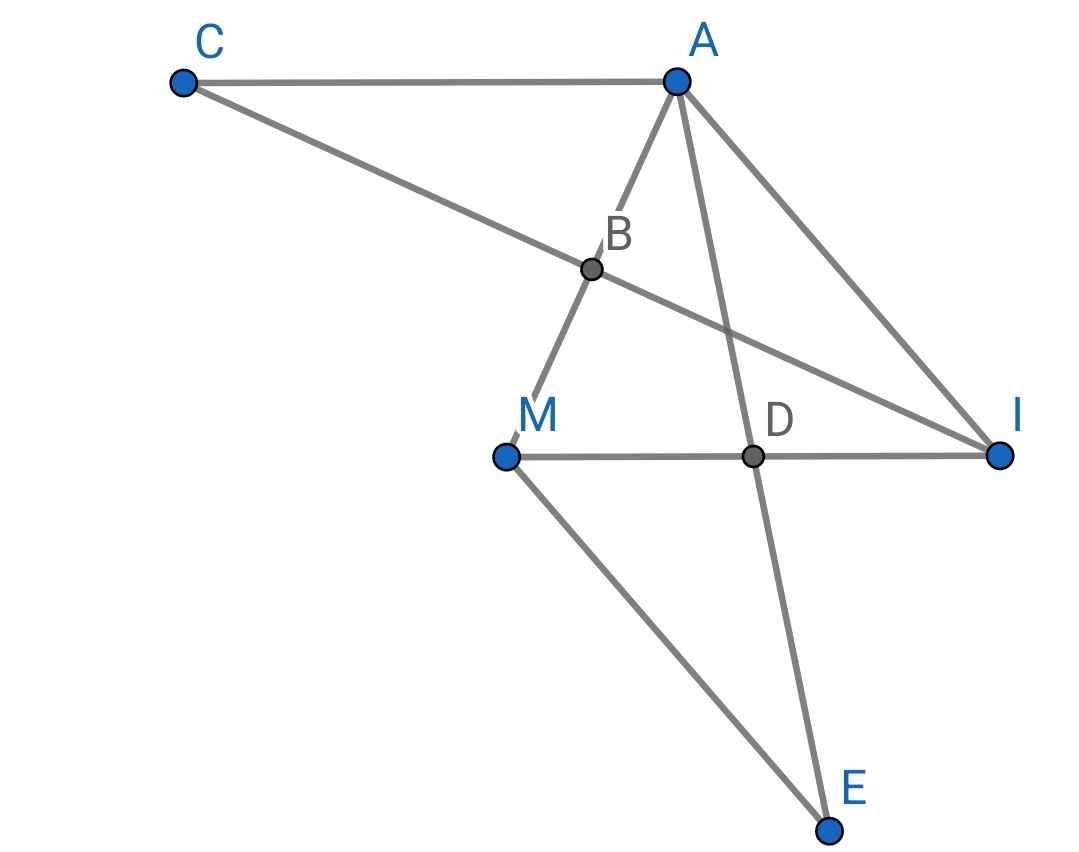
a) Do B là trung điểm của AM (gt)
⇒ BA = BM
Xét ∆ABC và ∆MBI có:
BA = BM (cmt)
∠ABC = ∠MBI (đối đỉnh)
BC = BI (gt)
⇒ ∆ABC = ∆MBI (c-g-c)
⇒ AC = MI (hai cạnh tương ứng)
Do ∆ABC = ∆MBI (cmt)
⇒ ∠ACB = ∠MIB (hai góc tương ứng)
Mà ∠ACB và ∠MIB là hai góc so le trong
⇒ AC // MI
b) Do D là trung điểm của MI (gt)
⇒ DM = DI
Xét ∆ADI và ∆EDM có:
DI = DM (cmt)
∠ADI = ∠EDM (đối đỉnh)
AD = DE (gt)
⇒ ∆ADI = ∆EDM (c-g-c)
⇒ AI = ME (hai cạnh tương ứng)
Do ∆ADI = ∆EDM (cmt)
⇒ ∠AID = ∠EMD (hai góc tương ứng)
Mà ∠AID và ∠EMD là hai góc so le trong
⇒ AI // ME
c) Đề sai, em xem lại đề nhé

a) Sửa đề: Chứng minh ∆ABE = ∆DBE
Xét hai tam giác vuông: ∆ABE và ∆DBE có:
BE là cạnh chung
BA = BD (gt)
⇒ ∆ABE = ∆DBE (cạnh huyền - góc nhọn)
b) Do ∆ABE = ∆DBE (cmt)
⇒ AE = DE (hai cạnh tương ứng)
∆CDE vuông tại D
EC là cạnh huyền nên là cạnh lớn nhất
⇒ DE < EC
Mà AE = DE (cmt)
⇒ AE < EC
c) Gọi G là giao điểm của AD và BE
Do ∆ABE = ∆DBE (cmt)
⇒ ∠ABE = ∠DBE (hai góc tương ứng)
⇒ ∠ABG = ∠DBG
Xét ∆ABG và ∆DBG có:
BA = BD (gt)
∠ABG = ∠DBG (cmt)
BG là cạnh chung
⇒ ∆ABG = ∆DBG (c-g-c)
⇒ ∠AGB = ∠DGB (hai góc tương ứng)
Mà ∠AGB + ∠DGB = 180⁰ (kề bù)
⇒ ∠AGB = ∠DGB = 180⁰ : 2 = 90⁰
⇒ BG ⊥ AD (1)
Do ∆ABG = ∆DBG (cmt)
⇒ AG = DG (hai cạnh tương ứng)
⇒ G là trung điểm của AD (2)
Từ (1) và (2) ⇒ BG là đường trung trực của AD
⇒ BE là đường trung trực của AD
d) Xét hai tam giác vuông: ∆EDC và ∆EAF có:
DE = AE (cmt)
∠DEC = ∠AEF (đối đỉnh)
⇒ ∆EDC = ∆EAF (cạnh góc vuông - góc nhọn kề)
⇒ EC = EF (hai cạnh tương ứng)
∆EFC có:
EC = EF (cmt)
⇒ ∆EFC cân tại E
cho S= \(1\times2^0+2\times2^1+3\times3^2+...+2019\times2^{2018}\)
so sánh S với 22018 x 2019 + 2019

Lời giải:
** Sửa lại đề:
$S=1.2^0+2.2^1+3.2^2+...+2019.2^{2018}$
$2S=1.2^1+2.2^2+3.2^3+...+2018.2^{2018}+2019.2^{2019}$
$\Rightarrow 2S-S=2019.2^{2019}-(2^0+2^1+2^2+2^3+...+2^{2018})$
$\Rightarrow S=2019.2^{2019}-(2^0+2^1+2^2+2^3+...+2^{2018})$
Xét:
$M=2^0+2^1+2^2+..+2^{2018}$
$2M=2^1+2^2+2^3+...+2^{2019}$
$\Rightarrow 2M-M=2^{2019}-2^0$
$\Rightarrow M=2^{2019}-1$
$S=2019.2^{2019}-M = 2019.2^{2019}-(2^{2019}-1)=2018.2^{2019}+1$
Xét hiệu:
$S-(2019.2^{2018}+2019)=2018.2^{2019}+1-2019.2^{2018}-2019$
$=2^{2018}(2018.2-2019)+1-2019$
$=2^{2018}.2017-2018>0$
$\Rightarrow S> 2019.2^{2018}+2019$

Lời giải:
a.
Đặt $\frac{a}{5}=\frac{b}{4}=k\Rightarrow a=5k, b=4k$
Khi đó:
$a^2-b^2=1$
$\Rightarrow (5k)^2-(4k)^2=1$
$\Rightarrow 9k^2=1\Rightarrow k^2=\frac{1}{9}\Rightarrow k=\frac{1}{3}$ hoặc $k=\frac{-1}{3}$
Nếu $k=\frac{1}{3}$ thì:
$a=5k=\frac{5}{3}; b=4k=\frac{4}{3}$
Nếu $k=\frac{-1}{3}$ thì:
$a=5k=\frac{-5}{3}; b=4k=\frac{-4}{3}$
b.
Đặt $\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=k$
$\Rightarrow a=2k; b=3k; c=4k$
Khi đó:
$a^2-b^2+2c^2=108$
$\Rightarrow (2k)^2-(3k)^2+2(4k)^2=108$
$\Rightarrow 27k^2=108$
$\Rightarrow k^2=4\Rightarrow k=\pm 2$
Nếu $k=2$ thì:
$a=2k=4; b=3k=6; c=4k=8$
Nếu $k=-2$ thì:
$a=2k=-4; b=3k=-6; c=4k=-8$

Lần sau bạn lưu ý đăng đầy đủ yêu cầu đề bài.
Lời giải:
$E=1.1+2.2+3.3+...+99^2+100^2$
$=1(2-1)+2(3-1)+3(4-1)+....+99(100-1)+100(101-1)$
$=\underbrace{(1.2+2.3+3.4+...+99.100+100.101)}_{M}-\underbrace{(1+2+3+...+100)}_{N}$
Xét:
$N=100(100+1):2=5050$
$M = 1.2+2.3+3.4+....+99.100+100.101$
$3M = 1.2.3+2.3(4-1)+3.4(5-2)+...+99.100(101-98)+100.101(102-99)$
$=1.2.3+2.3.4+3.4.5+.....+99.100.101+100.101.102-(1.2.3+2.3.4+....+98.99.100+99.100.101)$
$=100.101.102$
$\Rightarrow M = \frac{100.101.102}{3}=343400$
$\Rightarrow E=M-N=343400-5050=338350$