1. Một hộp có $10$ chiếc thẻ cùng loại, mỗi thẻ ghi một trong các số $0, 1, 2, 3, …, 9$. Rút ngẫu nhiên một chiếc thẻ trong hộp.
a) Viết tập hợp $A $ gồm các kết quả có thể xảy ra đối với số xuất hiện trên thẻ được rút ra.
b) Liệt kê các kết quả có lợi cho biến cố $B$: “Số xuất hiện trên thẻ được rút là số nguyên tố.”
Tính xác suất của biến cố $B$.
2. Cửa hàng X thống kê lại số lượt khách đến cửa hàng tại các thời điểm trong ngày bằng biểu đồ bên dưới.
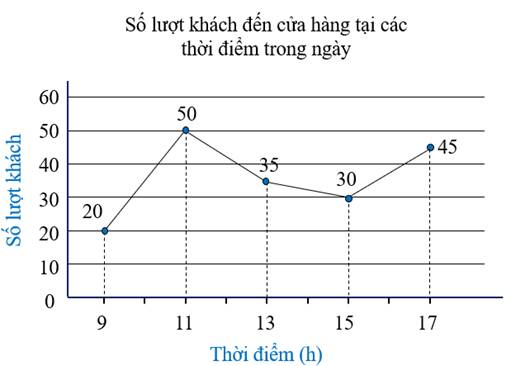
a) Cửa hàng đông khách nhất vào thời điểm nào? Vắng khách nhất vào thời điểm nào?
b) Số lượt khách đến cửa hàng từ $15$ giờ đến $17$ giờ tăng hay giảm bao nhiêu lượt khách?


2.
a) Cửa hàng đông khách nhất vào thời điểm 11 giờ
Cửa hàng vắng khách nhất vào thời điểm 9 giờ.
b) Số lượt khách đến cửa hàng từ 15 giờ đến 17 giờ tăng 15 lượt khách.
2.
a) Cửa hàng đông khách nhất vào thời điểm 11 giờ
Cửa hàng vắng khách nhất vào thời điểm 9 giờ.
b) Số lượt khách đến cửa hàng từ 15 giờ đến 17 giờ tăng 15 lượt khách.