\(\left|x-2\right|>=0\forall x\)

\(\left|y-1\right|>=0\forall y\)

\(\left(x+y+z-2\right)^{2024}>=0\forall x,y,z\)

Do đó: \(\left|x-2\right|+\left|y-1\right|+\left(x+y-z-2\right)^{2024}>=0\forall x,y,z\)

Dấu '=' xảy ra khi \(\left\{{}\begin{matrix}x-2=0\\y-1=0\\x+y-z-2=0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x=2\\y=1\\z=x+y-2=2+1-2=1\end{matrix}\right.\)

a: Xét ΔABD và ΔACD có

AB=AC

\(\widehat{BAD}=\widehat{CAD}\)

AD chung

Do đó: ΔABD=ΔACD

b: ta có: ΔABD=ΔACD

=>DB=DC

=>D là trung điểm của BC

c: Ta có: \(\widehat{ABC}+\widehat{ABM}=180^0\)(hai góc kề bù)

\(\widehat{ACB}+\widehat{ACN}=180^0\)(hai góc kề bù)

mà \(\widehat{ABC}=\widehat{ACB}\)

nên \(\widehat{ABM}=\widehat{ACN}\)

Xét ΔABM và ΔACN có

AB=AC

\(\widehat{ABM}=\widehat{ACN}\)

BM=CN

Do đó: ΔABM=ΔACN

d: Ta có: ΔABM=ΔACN

=>AM=AN

=>ΔAMN cân tại A

e: ta có: ΔABM=ΔACN

=>\(\widehat{MAB}=\widehat{NAC}\)

Xét ΔAKB vuông tại K và ΔAHC vuông tại H có

AB=AC

\(\widehat{KAB}=\widehat{HAC}\)

Do đó: ΔAKB=ΔAHC

f: Ta có: ΔAKB=ΔAHC

=>AK=AH

Xét ΔAMN có \(\dfrac{AK}{AM}=\dfrac{AH}{AN}\)

nên KH//MN

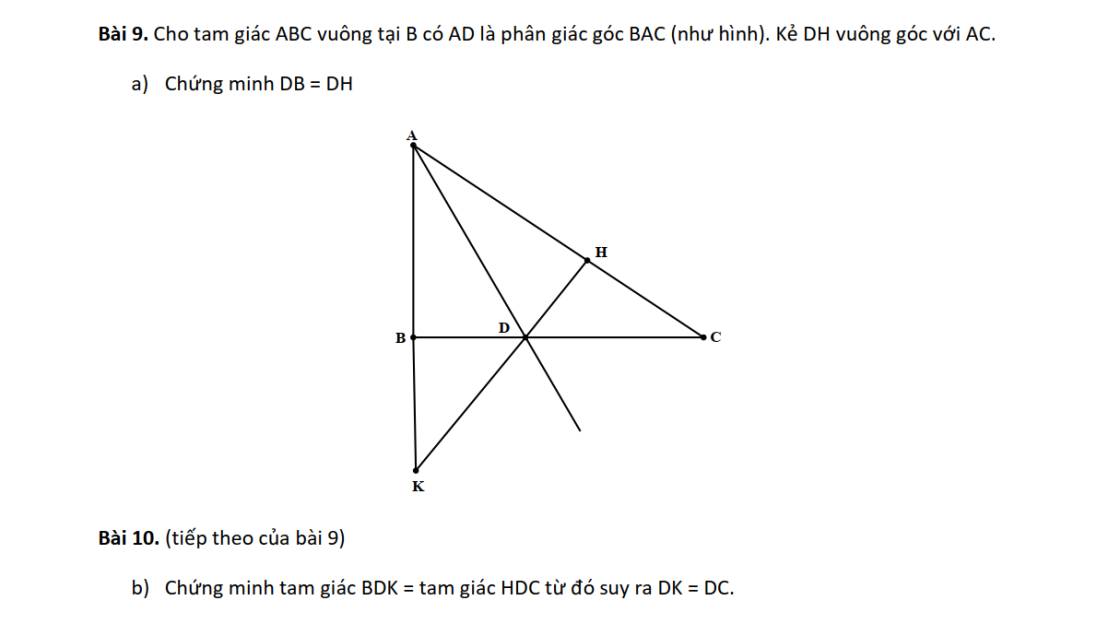
a: Xét ΔABD vuông tại B và ΔAHD vuông tại H có

AD chung

\(\widehat{BAD}=\widehat{HAD}\)

Do đó: ΔABD=ΔAHD

=>DB=DH

b: Xét ΔDBK vuông tại B và ΔDHC vuông tại H có

DB=DH

\(\widehat{BDK}=\widehat{HDC}\)(hai góc đối đỉnh)

Do đó: ΔDBK=ΔDHC

=>DK=DC

Kẻ IH là phân giác của góc BIC

Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)

=>\(\widehat{ABC}+\widehat{ACB}=180^0-60^0=120^0\)

=>\(2\cdot\left(\widehat{IBC}+\widehat{ICB}\right)=120^0\)

=>\(\widehat{IBC}+\widehat{ICB}=60^0\)

Xét ΔIBC có \(\widehat{IBC}+\widehat{ICB}+\widehat{BIC}=180^0\)

=>\(\widehat{BIC}+60^0=180^0\)

=>\(\widehat{BIC}=120^0\)

Ta có: \(\widehat{BIC}+\widehat{BIF}=180^0\)(hai góc kề bù)

=>\(\widehat{BIF}+120^0=180^0\)

=>\(\widehat{BIF}=60^0\)

Ta có: \(\widehat{BIF}=\widehat{EIC}\)(hai góc đối đỉnh)

mà \(\widehat{BIF}=60^0\)

nên \(\widehat{EIC}=60^0\)

IH là phân giác của góc BIC

=>\(\widehat{BIH}=\widehat{CIH}=\dfrac{\widehat{BIC}}{2}=60^0\)

Xét ΔFBI và ΔHBI có

\(\widehat{FBI}=\widehat{HBI}\)

BI chung

\(\widehat{FIB}=\widehat{HIB}\left(=60^0\right)\)

Do đó: ΔFBI=ΔHBI

=>IF=IH

Xét ΔIHC và ΔIEC có

\(\widehat{HIC}=\widehat{EIC}\)

IC chung

\(\widehat{HCI}=\widehat{ECI}\)

Do đó: ΔIHC=ΔIEC

=>IH=IE

mà IH=IF

nên IE=IF

\(x:5=y:4\Rightarrow\dfrac{x}{5}=\dfrac{y}{4}\)

\(y:2=z:3\Rightarrow\dfrac{y}{4}=\dfrac{z}{6}\)

\(\Rightarrow\dfrac{x}{5}=\dfrac{y}{4}=\dfrac{z}{6}\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{x}{5}=\dfrac{y}{4}=\dfrac{z}{6}=\dfrac{x+y+z}{5+4+6}=\dfrac{90}{15}=6\)

\(\Rightarrow\dfrac{x}{5}=6\Rightarrow x=30\)

\(\Rightarrow\dfrac{y}{4}=6\Rightarrow y=24\)

\(\Rightarrow\dfrac{z}{6}=6\Rightarrow z=36\)

Gọi số gạo ban đầu trong kho 1;kho 2;kho 3 lần lượt là a(tấn),b(tấn),c(tấn)
(ĐK: a>0; b>0; c>0)

Số gạo của ba kho lần lượt tỉ lệ với \(1,3;2+\dfrac{1}{2}=2,5;6,5\) nên ta có: \(\dfrac{a}{1,3}=\dfrac{b}{2,5}=\dfrac{c}{6,5}\)

=>\(\dfrac{a}{13}=\dfrac{b}{25}=\dfrac{c}{65}\)

Số gạo của kho thứ hai nhiều hơn kho thứ nhất 43,2 tấn nên b-a=43,2

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{a}{13}=\dfrac{b}{25}=\dfrac{c}{65}=\dfrac{b-a}{25-13}=\dfrac{43.2}{12}=3.6\)

=>\(a=3,6\cdot13=46,8;b=25\cdot3,6=90;c=3,6\cdot65=234\)

Số gạo bán được ở kho 1 là:

\(46,8\cdot40\%=18,72\left(tân\right)\)

Số gạo bán được ở kho 2 là:

\(90\cdot30\%=27\left(tấn\right)\)

Số gạo bán được ở kho 3 là:

\(234\cdot25\%=58,5\left(tấn\right)\)

Số gạo bán được là:

18,72+27+58,5=104,22(tấn)

\(4,5:0,3=2,25:\left(0,1x\right)\)

=>\(2,25:\left(0,1x\right)=15\)

=>\(0,1\cdot x=2,25:15=0,15\)

=>\(x=0,15:0,1=1,5\)

Ta có: \(\dfrac{a-1}{2}=\dfrac{b-2}{3}=\dfrac{c-3}{4}\) và \(a-2b-3c=14\) \((*)\)

Áp dụng tính chất của dãy tỉ số bằng nhau và \((*)\), ta được:

\(\dfrac{a-1}{2}=\dfrac{b-2}{3}=\dfrac{c-3}{4}=\dfrac{2\left(b-2\right)}{6}=\dfrac{3\left(c-3\right)}{12}\)

\(=\dfrac{\left(a-1\right)-2\left(b-2\right)-3\left(c-3\right)}{2-6-12}\)

\(=\dfrac{a-1-2b+4-3c+9}{-16}\)

\(=\dfrac{\left(a-2b-3c\right)+\left(-1+4+9\right)}{-16}\)

\(=\dfrac{14+12}{-16}=-\dfrac{13}{8}\)

Suy ra: \(\dfrac{a-1}{2}=\dfrac{-13}{8}\)

\(\Rightarrow8\left(a-1\right)=-13\cdot2\)

\(\Rightarrow8a-8=-26\)

\(\Rightarrow8a=-26+8\)

\(\Rightarrow8a=-18\Rightarrow a=-\dfrac{9}{4}\)

a: Xét ΔABI và ΔACI có

AB=AC

BI=CI

AI chung

Do đó; ΔABI=ΔACI

b: Ta có: ΔAIB=ΔAIC

=>\(\widehat{AIB}=\widehat{AIC}\)

mà \(\widehat{AIB}+\widehat{AIC}=180^0\)(hai góc kề bù)

nên \(\widehat{AIB}=\widehat{AIC}=\dfrac{180^0}{2}=90^0\)

=>AI\(\perp\)BC

c: Xét ΔABC có

AI là đường trung tuyến

G là trọng tâm

Do đó: \(AG=\dfrac{2}{3}AI=\dfrac{2}{3}\cdot12=8\left(cm\right)\)

Ta có: AG+GI=AI

=>GI+8=12

=>GI=4(cm)