3 đường cao

3 đường cao

Lời giải:
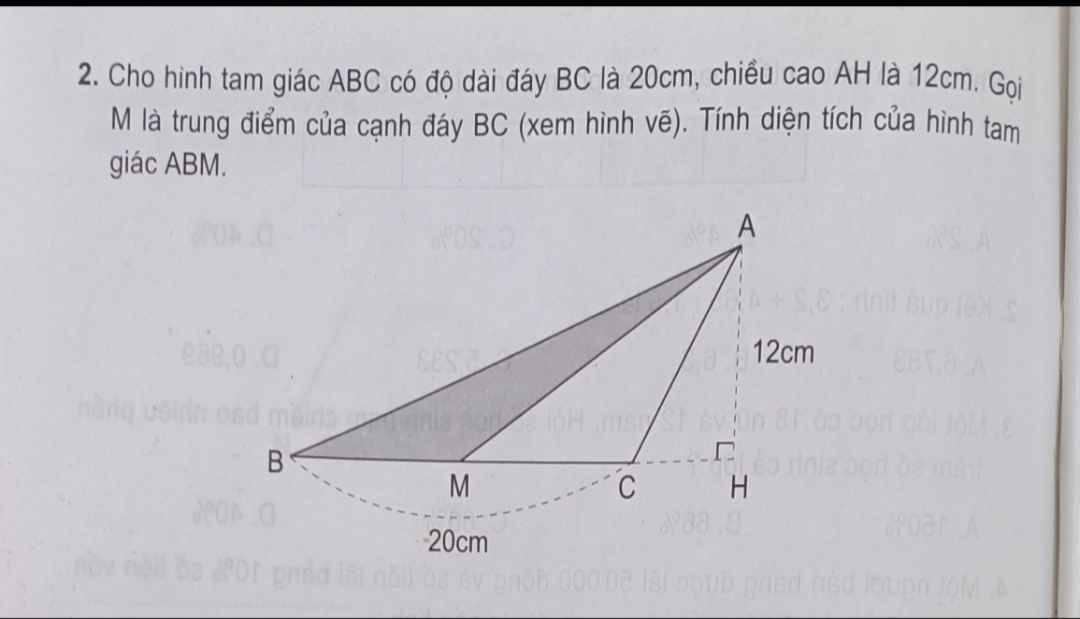
$S_{ABC}=AH\times BC:2=12\times 20:2=120$ (cm²)

$\frac{S_{ABM}}{S_{ABC}}=\frac{BM}{BC}=\frac{1}{2}$ (do $M$ là trung điểm $BC$)

$S_{ABM}=\frac{1}{2}\times S_{ABC}=\frac{1}{2}\times 120=60$ (cm²)

Từ 25 đến 129 có số 30

Do đó chữ số tận cùng của tích là chữ số 0

\(25\rightarrow129\) có số \(30\)

Lấy \(0\) nhân với tận cùng của các số còn lại vẫn bằng \(0\)

Vậy tích các STN từ \(25\) đến \(129\) có chữ số tận cùng là \(0\)

\(7⋮\left(x+1\right)\Rightarrow\left(x+1\right)\inƯ\left(7\right)=\left\{-7;-1;1;7\right\}\\ Có:x+1=-7\Rightarrow x=-8\\ x+1=-1\Rightarrow x=-2\\ x+1=1\Rightarrow x=0\\ x+1=7\Rightarrow x=6\\ Vậy:x\in\left\{-8;-2;0;6\right\}\)

Ta có:

\(7⋮\left(x+1\right)\Rightarrow x+1\inƯ\left(7\right)=\left\{\pm1;\pm7\right\}\)

Ta có bảng sau:

Vậy \(x\in\left\{0;-2;6;-8\right\}\)

\(\Leftrightarrow\dfrac{3}{1.4}+\dfrac{3}{4.7}+...+\dfrac{3}{x\left(x+3\right)}=\dfrac{375}{376}\)

\(\Leftrightarrow1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{7}+...+\dfrac{1}{x}-\dfrac{1}{x+3}=\dfrac{375}{376}\)

\(\Leftrightarrow1-\dfrac{1}{x+3}=\dfrac{375}{376}\)

\(\Leftrightarrow\dfrac{1}{x+3}=1-\dfrac{375}{376}=\dfrac{1}{376}\)

\(\Rightarrow x+3=376\)

\(\Rightarrow x=373\)

2964794 : 1111 = 2668,5823

Cho 1 like

=2668,582358

cho like

a.

Do M là trung điểm SA, O là trung điểm AC

\(\Rightarrow OM\) là đường trung bình tam giác SAC \(\Rightarrow OM||SC\Rightarrow OM||\left(SBC\right)\) (1)

N là trung điểm CD, O là trung điểm AC \(\Rightarrow ON\) là đường trung bình ACD

\(\Rightarrow ON||AD\Rightarrow ON||BC\Rightarrow ON||\left(SBC\right)\) (2)

Mà \(ON\cap OM=O\)  ; \(OM;ON\in\left(OMN\right)\) (3)

(1);(2);(3) \(\Rightarrow\left(OMN\right)||\left(SBC\right)\)

b.

J cách đều AB, CD \(\Rightarrow J\) thuộc đường thẳng d qua O và song song AB, CD

- Nếu J trùng O \(\Rightarrow OI\) là đường trung bình tam giác SBD \(\Rightarrow OI||SB\Rightarrow OI||\left(SAB\right)\)

Hay \(IJ||\left(SAB\right)\)

- Nếu J không trùng O, ta có \(\left\{{}\begin{matrix}IO||SB\left(đtb\right)\Rightarrow IO||\left(SAB\right)\\d||AB\Rightarrow IJ||AB\Rightarrow OJ||\left(SAB\right)\end{matrix}\right.\)

\(\Rightarrow\left(OIJ\right)||\left(SAB\right)\Rightarrow IJ||\left(SAB\right)\)

a.

Do M là trung điểm SA, O là trung điểm AC

$\Rightarrow OM$ là đường trung bình tam giác SAC $\Rightarrow OM||SC\Rightarrow OM||\left(SBC\right)$ (1)

N là trung điểm CD, O là trung điểm AC $\Rightarrow ON$ là đường trung bình ACD

$\Rightarrow ON||AD\Rightarrow ON||BC\Rightarrow ON||\left(SBC\right)$ (2)

Mà $ON\cap OM=O$  ; $OM;ON\in \left(OMN\right)$ (3)

(1);(2);(3) $\Rightarrow \left(OMN\right)||\left(SBC\right)$

b.

J cách đều AB, CD $\Rightarrow J$ thuộc đường thẳng d qua O và song song AB, CD

- Nếu J trùng O $\Rightarrow OI$ là đường trung bình tam giác SBD $\Rightarrow OI||SB\Rightarrow OI||\left(SAB\right)$

Hay $IJ||\left(SAB\right)$

- Nếu J không trùng O, ta có {��∣∣��(đ��)⇒��∣∣(���)�∣∣��⇒��∣∣��⇒��∣∣(���){IO∣∣SB(đtb)⇒IO∣∣(SAB)d∣∣AB⇒IJ∣∣AB⇒OJ∣∣(SAB)​

$\Rightarrow \left(OIJ\right)||\left(SAB\right)\Rightarrow IJ||\left(SAB\right)$

10B

11B

12B

C