
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a, \(\frac{x+5}{x+3}< 1\Leftrightarrow x+5< x+3\)
\(\Leftrightarrow5< 3\)( vô lí vaichuong =))
Vậy ko có giá trị x thỏa mãn đề bài
b, \(\frac{x+3}{x+4}>1\Leftrightarrow x+3>x+4\)
\(\Leftrightarrow3>4\)( vô lí )
Vậy ko có giá trị x thỏa mãn đề bài

Cách 1 : \(\left(x-1\right)^{2019}+\left(x-1\right)^{2020}=0\)
Vì \(\left(x-1\right)^{2019}\ge0\forall x;\left(x-1\right)^{2020}\ge0\forall x\)
\(\Rightarrow\left(x-1\right)^{2019}+\left(x-1\right)^{2020}\ge0\forall x\)
Dấu ''='' xảy ra <=> x = 1
Cách 2 : \(\left(x-1\right)^{2019}+\left(x-1\right)^{2020}=0\)
\(\Leftrightarrow\left(x-1\right)^{2019}\left[1+\left(x-1\right)\right]=0\)
\(\Leftrightarrow x\left(x-1\right)^{2019}=0\Leftrightarrow x=0;1\)

@Khuê =)) vậy là bn ''gà'' hơn mk rồi.
\(f\left(x\right)=7\)hay \(9x^2-2=7\)
\(\Leftrightarrow9x^2=9\Leftrightarrow x^2=1\Leftrightarrow x=\pm1\)
\(f\left(x\right)=1\)hay \(9x^2-2=1\Leftrightarrow x^2=\frac{1}{3}\Leftrightarrow x=\pm\sqrt{\frac{1}{3}}\)


a) Ta có \(\frac{a+b-3c}{c}=\frac{b+c-3a}{a}=\frac{c+a-3b}{b}\)
=> \(\frac{a+b-3c}{c}+4=\frac{b+c-3a}{a}+4=\frac{c+a-3b}{b}+4\)
=> \(\frac{a+b+c}{c}=\frac{a+b+c}{a}=\frac{a+b+c}{b}\)
Vì a;b;c > 0
=> a + b + c > 0
=> \(\frac{1}{c}=\frac{1}{a}=\frac{1}{b}\)=> a = b = c (đpcm)
2) Đặt \(\frac{a}{2016}=\frac{b}{2017}=\frac{c}{2018}=k\)
=> \(\hept{\begin{cases}a=2016k\\b=2017k\\c=2018k\end{cases}}\)
Khi đó M = 4(a - b)(b - c) - (c - a)2
= 4(2016k - 2017k)(2017k - 2018k) - (2018k - 2016k)2
= 4(-k).(-k) - (2k)2
= 4k2 - 4k2 = 0

\(\frac{4}{11.16}+\frac{4}{16.21}+\frac{4}{21.26}+...+\frac{4}{61.66}\)
= \(\frac{4}{5}\left(\frac{5}{11.16}+\frac{5}{16.21}+\frac{5}{21.26}+...+\frac{5}{61.66}\right)\)
\(=\frac{4}{5}\left(\frac{1}{11}-\frac{1}{16}+\frac{1}{16}-\frac{1}{21}+\frac{1}{21}-\frac{1}{26}+...+\frac{1}{61}-\frac{1}{66}\right)\)
\(=\frac{4}{5}\left(\frac{1}{11}-\frac{1}{66}\right)=\frac{4}{5}.\frac{5}{66}=\frac{2}{33}\)

a)\(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+...+\frac{1}{19.21}\)
\(=\frac{1}{2}\left(\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+...+\frac{2}{19.21}\right)\)
\(=\frac{1}{2}\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{19}-\frac{1}{21}\right)\)
\(=\frac{1}{2}\left(1-\frac{1}{21}\right)=\frac{1}{2}.\frac{20}{21}=\frac{10}{21}\)
b) Ta có A = \(\frac{1}{1.3}+\frac{1}{3.5}+...+\frac{1}{\left(2n-1\right)\left(2n+1\right)}\)
\(=\frac{1}{2}\left(\frac{2}{1.3}+\frac{2}{3.5}+...+\frac{2}{\left(2n-1\right)\left(2n+1\right)}\right)\)
\(=\frac{1}{2}\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+...+\frac{1}{2n-1}-\frac{1}{2n+1}\right)\)
\(=\frac{1}{2}\left(1-\frac{1}{2n+1}\right)=\frac{1}{2}-\frac{1}{2\left(2n+1\right)}< \frac{1}{2}\)(đpcm)
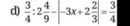
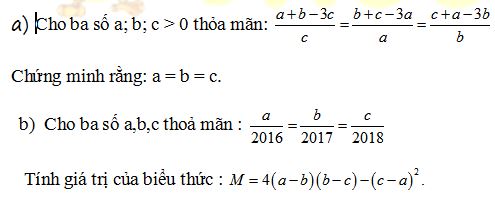 Giúp mình với
Giúp mình với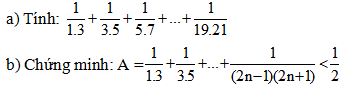 Giúp mình với
Giúp mình với