Hình có hai góc đối bằng nhau là hình bình hành
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) \(\dfrac{9}{4}-3y+y^2\)
\(=\left(\dfrac{3}{2}\right)^2-3y+y^2\)
\(=y^2-2\cdot\dfrac{3}{2}\cdot y+\left(\dfrac{3}{2}\right)^2\)
\(=\left(y-\dfrac{3}{2}\right)^2\)
b) \(x^3+6x^2y+12xy^2+8y^3\)
\(=x^3+6x^2y+12xy^2+\left(2y\right)^3\)
\(=x^3+3\cdot x^2\cdot2y+3\cdot x\cdot\left(2y\right)^2+\left(2y\right)^3\)
\(=\left(x+2y\right)^2\)

Với \(n=4\), ta chỉ ra một trường hợp sau thỏa mãn:
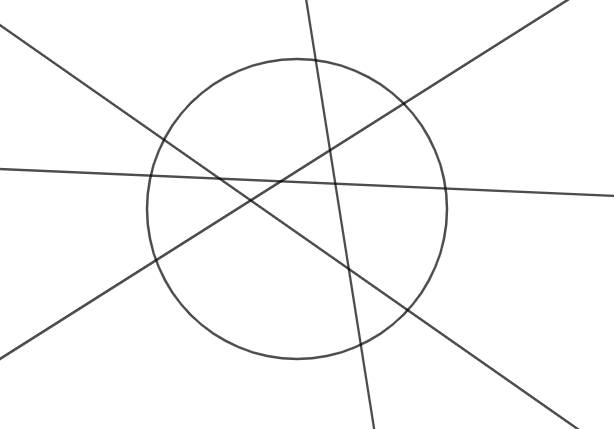
Với \(n\le3\), ta xét trường hợp mà n đường thẳng chia hình tròn thành nhiều miền nhất. (Tức là không có 3 đường nào đồng quy và không có 2 đường thẳng nào song song hoặc cắt nhau bên ngoài hình tròn). Khi đó đường tròn bị chia thành tối đa 7 miền, không thỏa mãn.
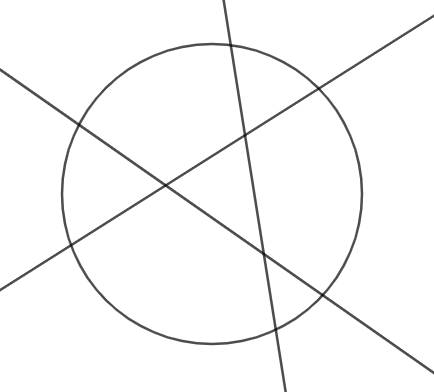
Vậy \(min_n=4\)

Xét hệ trục tọa độ Oxy với O trùng với vị trí ban đầu của Peter, Ox trùng với hướng Tây - Đông, Oy trùng với phương Nam - Bắc.
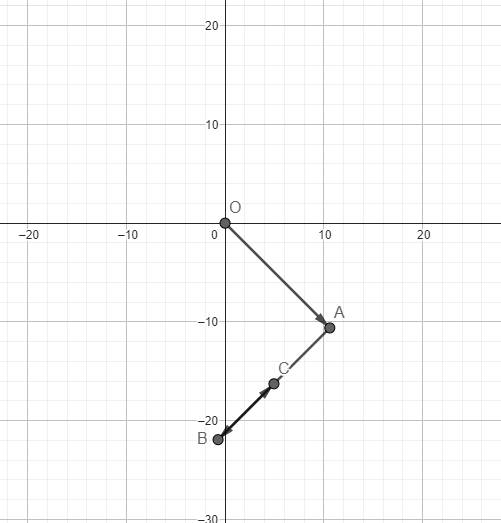
Gọi A, B, C tương ứng là vị trí của Peter sau lần đi thứ nhất, thứ 2 và cuối cùng.
Ta có \(OA=16km\), \(\widehat{OAC}=90^o\) và \(AC=AB-BC=16-8=8\left(km\right)\)
\(\Rightarrow OC=\sqrt{15^2+8^2}=17\left(km\right)\)
Vậy sau lần đi cuối cùng, Peter cách vị trí ban đầu 17km.

Gọi mã là \(\overline{mXn}\)
Ta thấy có 10 cách chọn \(m\), 10 cách chọn \(n\) và 26 cách chọn X nên sẽ có nhiều nhất \(10.10.26=2600\) mật mã khác nhau.
Vậy công ty đó có thể dán mã lên nhiều nhất 2600 loại sản phẩm khác nhau.

Gọi số bộ ghép hình là x; số búp bê là y và số gấu bông là z ta có
\(\left\{{}\begin{matrix}x+y+z=14\\8x+4y+5z=92\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8x+8y+8z=112\left(1\right)\\8x+4y+5z=92\left(2\right)\end{matrix}\right.\) Trừ 2 vế của (1) cho (2)
\(\Rightarrow4y+3z=20\Leftrightarrow y=\dfrac{20-3z}{4}=5-\dfrac{3z}{4}\)
Do \(y\in\) N* => 4 phải là UC(3z)
Đồng thời \(y>0\Rightarrow5-\dfrac{3z}{4}>0\Leftrightarrow3z< 20\Leftrightarrow z< \dfrac{20}{3}\Rightarrow z\le6\)
=> Giá trị z thỏa mãn là z=4

X : Y = 8 ⇒ X/8 = Y/1 ⇒ X/16 = Y/2 (1)
Z : X = 3 : 16 ⇒ Z/3 = X/16 (2)
Từ (1) và (2) ⇒ X/16 = Y/2 = Z/3
Áp dụng tính chất của dãy tỉ số bằng nhau, ta có:
X/16 = Y/2 = Z/3 = (X + Y + Z)/(16 + 2 + 3) = 150/21 = 50/7
X/16 = 50/7 ⇒ X = 50/7 . 16 = 800/7
Vậy X = 800/7

Gọi chiều dài đoàn tàu ngắn là x thì chiều dài đoàn tàu dài là 2x
Giả sử 1 trong 2 đoàn tàu đứng yên thì vận tốc của đoàn tàu còn lại là
74+70=144 km/h
Hai đoàn tàu đi ngược chiều nhau mất 6 s là khoảng thời gian khi đầu của 2 đoàn tàu bắt đầu gặp nhau cho đến khi đuôi của 2 đoàn tàu gặp nhau
Khi đó đoàn tàu được coi là chuyển động đã đi được quãng đường bằng tổng chiều dài của 2 đoàn tàu và là
x+2x=3x
Ta có phương trình
\(\dfrac{3x}{144}=\dfrac{6}{3600}=\dfrac{1}{600}\Leftrightarrow1800x=144\Leftrightarrow x=0,08km=80m\)
Chiều dài đoàn tàu dài là
2.80=160 m
Bạn cần ghi đầy đủ đề để mọi người dễ dàng hỗ trợ hơn.