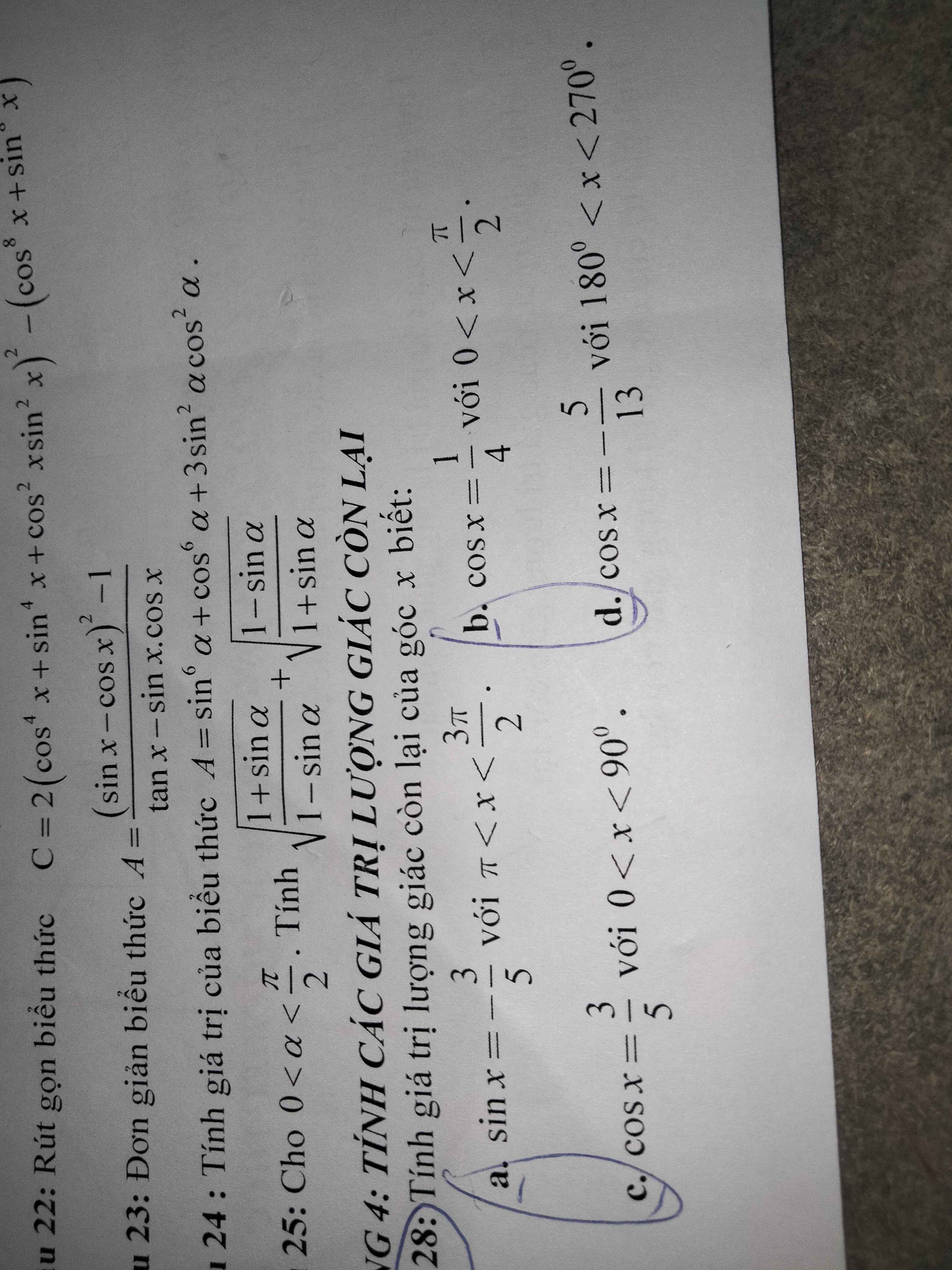
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Có \(AC=AD\sqrt{2}=a\sqrt{2}\)
\(SA\perp\left(ABCD\right)\Rightarrow SA\perp AC\) \(\Rightarrow\Delta SAC\) vuông tại A.
\(\Rightarrow SA=\sqrt{SC^2-AC^2}=\sqrt{\left(a\sqrt{3}\right)^2-\left(a\sqrt{2}\right)^2}=a\)
\(\Rightarrow V_{S.ABCD}=\dfrac{1}{3}.S_{ABCD}.SA=\dfrac{1}{3}.AD^2.SA=\dfrac{1}{3}.a^2.a=\dfrac{a^3}{3}\)

Lời giải:
Gọi cạnh hình lập phương là $a$.
Vì $AD\parallel A'D'$ nên:
$\angle (A'D', C'D)=\angle (AD, C'D)=\widehat{ADC'}$
Ta thấy:
$AD=a$
$DC'=\sqrt{DD'^2+D'C'^2}=\sqrt{a^2+a^2}=\sqrt{2}a$
$AC'=\sqrt{AA'^2+A'C'^2}=\sqrt{a^2+2a^2}=\sqrt{3}a$
$\Rightarrow AD^2+DC'^2=AC'^2$
$\Rightarrow ADC'$ là tam giác vuông tại $D$ (theo định lý Pitago đảo)
$\Rightarrow \angle (A'D', C'D)=\widehat{ADC'}=90^0$

Gọi số năm để người đó nhận được tổng số tiền nhiều 300 triệu là x(năm)
(Điều kiện: x>0)
Sau x năm, số tiền người đó nhận được sẽ là:
\(100\cdot10^6\left(1+0,06\right)^x\left(đồng\right)\)
Theo đề, ta có: \(100\cdot10^6\left(1+0,06\right)^x=300\cdot10^6\)
=>\(\left(1+0,06\right)^x=3\)
=>\(x\simeq19\)
vậy: Sau 19 năm thì tổng số tiền người đó nhận được sẽ nhiều hơn 300 triệu

\(f'\left(x\right)=\left(\dfrac{x^2+3x-5}{x+2}\right)'\)
\(=\dfrac{\left(x^2+3x-5\right)'\left(x+2\right)-\left(x^2+3x-5\right)\left(x+2\right)'}{\left(x+2\right)^2}\)
\(=\dfrac{\left(2x+3\right)\left(x+2\right)-\left(x^2+3x-5\right)}{\left(x+2\right)^2}\)
\(=\dfrac{2x^2+7x+6-x^2-3x+5}{\left(x+2\right)^2}=\dfrac{x^2+4x+11}{\left(x+2\right)^2}\)
\(f'\left(1\right)=\dfrac{1^2+4\cdot1+11}{\left(1+2\right)^2}=\dfrac{16}{9}\)

\(s\left(t\right)=t^2-4t+3\)
=>\(v\left(t\right)=s'\left(t\right)=2t-4\)
=>\(a\left(t\right)=v'\left(t\right)=2\cdot1=2\)
=>a(4)=2

\(f\left(x\right)=-x^2+1\)
=>\(f'\left(x\right)=-2x\)
\(f\left(-2\right)=-\left(-2\right)^2+1=-4+1=-3\)
\(f'\left(-2\right)=-2\cdot\left(-2\right)=4\)
Phương trình tiếp tuyến của (P) tại x=-2 là:
y-f(-2)=f'(-2)(x+2)
=>y-(-3)=4(x+2)=4x+8
=>y=4x+8-3=4x+5

Sửa đề: Hình chóp S.ABC
a: ΔSAC vuông cân tại S
mà SH là đường trung tuyến
nên SH⊥AC tại H
(SAC)⊥(ABC)
(SAC) giao (ABC)=AC
SH⊂(SAC); SH⊥AC
Do đó: SH⊥(ABC)
b: Vì SH⊥(ABC)
nên \(\hat{SB;\left(BAC\right)}=\hat{BS;BH}=\hat{SBH}\)
Vì ΔABC đều có BH là đường trung tuyến
nên \(BH=AB\cdot\frac{\sqrt3}{2}=\frac{a\sqrt3}{2}\)
Xét ΔSHB vuông tại H có tan SBH=SH/HB
=>\(SH=BH\cdot\tan SBH=\frac{a\sqrt3}{2}\cdot\tan60=\frac{3a}{2}\)
Diện tích đáy ABC là:
\(S_{ABC}=AB^2\cdot\frac{\sqrt3}{4}=\frac{a^2\sqrt3}{4}\)
Thể tích khối chóp S.ABC là:
\(V=\frac13\cdot SH\cdot S_{ABC}=\frac13\cdot\frac{3a}{2}\cdot\frac{a^2\sqrt3}{4}=\frac{a^3\sqrt3}{8}\)

a, \(sin^2x+cos^2x=1\Leftrightarrow cos^2x=1-\dfrac{9}{25}=\dfrac{16}{25}\Leftrightarrow cosx=\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=-\dfrac{3}{5}:\left(\dfrac{4}{5}\right)=-\dfrac{3}{4}\)
\(cotx=-\dfrac{4}{3}\)
c, \(sin^2x+cos^2x=1\Leftrightarrow sin^2x=1-\dfrac{9}{25}=\dfrac{16}{25}\Leftrightarrow sinx=\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{4}{5}:\dfrac{3}{5}=\dfrac{4}{3}\)
\(cotx=\dfrac{3}{4}\)
b, \(cos^2x+sin^2x=1\Leftrightarrow sin^2x=1-\dfrac{1}{16}=\dfrac{15}{16}\Leftrightarrow sinx=\dfrac{\sqrt{15}}{4}\)
\(tanx=\dfrac{\sqrt{15}}{4}:\dfrac{1}{4}=\sqrt{15}\)
\(cotx=\dfrac{1}{\sqrt{15}}\)
d, \(sin^2x+cos^2x=1\Leftrightarrow sin^2x=1-\dfrac{25}{169}=\dfrac{144}{169}\Leftrightarrow sinx=\dfrac{12}{13}\)
\(tanx=\dfrac{12}{13}:\left(-\dfrac{5}{13}\right)=-\dfrac{12}{5}\)
\(cotx=-\dfrac{5}{12}\)
a: \(\Omega< x< \dfrac{3}{2}\Omega\)
=>cosx<0
Ta có: \(sin^2x+cos^2x=1\)
=>\(cos^2x=1-sin^2x=1-\left(\dfrac{3}{5}\right)^2=\dfrac{16}{25}\)
mà cosx<0
nên \(cosx=-\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{-3}{5}:\dfrac{-4}{5}=\dfrac{3}{4}\)
\(cotx=\dfrac{1}{tanx}=\dfrac{4}{3}\)
b: \(0< x< \dfrac{\Omega}{2}\)
=>sin x>0
\(sin^2x+cos^2x=1\)
=>\(sin^2x=1-\left(\dfrac{1}{4}\right)^2=\dfrac{15}{16}\)
mà sin x>0
nên \(sinx=\dfrac{\sqrt{15}}{4}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{\sqrt{15}}{4}:\dfrac{1}{4}=\sqrt{15}\)
\(cotx=\dfrac{1}{tanx}=\dfrac{1}{\sqrt{15}}=\dfrac{\sqrt{15}}{15}\)
c: 0<x<90 độ
=>sin x>0
\(sin^2x+cos^2x=1\)
=>\(sin^2x=1-\left(\dfrac{3}{5}\right)^2=\dfrac{16}{25}=\left(\dfrac{4}{5}\right)^2\)
mà sin x>0
nên \(sinx=\dfrac{4}{5}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{4}{5}:\dfrac{3}{5}=\dfrac{4}{3}\)
\(cotx=1:\dfrac{4}{3}=\dfrac{3}{4}\)
d: \(180^0< x< 270^0\)
=>sin x<0
\(sin^2x+cos^2x=1\)
=>\(sin^2x=1-\left(-\dfrac{5}{13}\right)^2=1-\dfrac{25}{169}=\dfrac{144}{169}\)
mà sin x<0
nên \(sinx=-\dfrac{12}{13}\)
\(tanx=\dfrac{sinx}{cosx}=\dfrac{-12}{13}:\dfrac{-5}{13}=\dfrac{12}{5}\)
\(cotx=\dfrac{1}{tanx}=\dfrac{5}{12}\)