Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A B C D H E
1/
Xét tg vuông AHD và tg vuông EHD có
HA=HD (gt); DH chung => tg AHD = tg EHD (hai tg vuông có 2 cạnh góc vuông bằng nhau)
\(\Rightarrow\widehat{DAH}=\widehat{DEH}\)
Xét tg vuông AHD có
\(\widehat{DAH}=90^o-\widehat{ADH}=90^o-30^o=60^o\)
\(\Rightarrow\widehat{DAH}=\widehat{DEH}=60^o\)
Xét tg ADE có
\(\widehat{ADE}=180^o-\left(\widehat{DAH}+\widehat{DEH}\right)=180^o-\left(60^o+60^o\right)=60^o\)
\(\Rightarrow\widehat{DAH}=\widehat{DEH}=\widehat{ADE}=60^o\)
=> tg ADE là tg đều
2/
Xét tg vuông AHD có
\(AH=\dfrac{AD}{2}=\dfrac{8}{2}=4cm\) (trong tg vuông cạnh đối diện góc \(30^o\) bằng nửa cạnh huyền)
\(\Rightarrow AH=EH=4cm\Rightarrow AH+EH=AE=8cm\)
\(DH=\sqrt{AD^2-AH^2}=\sqrt{8^2-4^2}=4\sqrt{3}cm\) (Pitago)
\(\Rightarrow S_{ADE}=\dfrac{1}{2}.AE.DH=\dfrac{1}{2}.8.4\sqrt{3}=16\sqrt{3}cm^2\)
\(\Rightarrow S_{ABCD}=\dfrac{\left(AB+CD\right).AH}{2}=\dfrac{\left(7+10\right).4}{2}=34cm^2\)

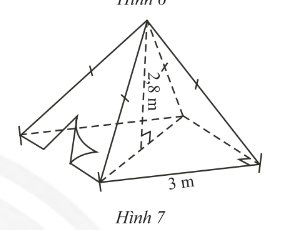
a) Thể tích không khí trong chiếc lều:
V = 3².2,8 : 3 = 8,4 (m³)
b) Diện tích toàn phần của lều:
3² + 4.3,18.3 : 2 = 28,08 (m²)
Số tiền mua vải:
28,08 . 150000 - 28,08 . 150000 . 5% = 4001400 (đồng)


Lời giải:
$T=(x+4)(x^2-4)(x+8)+8(x+3)^2$
$=(x+4)(x+2)(x-2)(x+8)+8(x+3)^2$
$=(x^2+6x+8)(x^2+6x-16)+8(x^2+6x+9)$
$=(a+8)(a-16)+8(a+9)$ (đặt $a=x^2+6x$)
$=a^2-56=(x^2+6x)^2-56\geq 0-56=-56$
Vậy $T_{\min}=-56$. Giá trị này đạt tại $x^2+6x=0\Leftrightarrow x=0$ hoặc $x=-6$



Lời giải:
a. $(x+2)^2=x^2+2.2.x+2^2=x^2+4x+4$
b. Đề đọc khó hiểu quá. Bạn viết lại bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề hơn.

\(3xy\left(2x^2y\right)\)
\(=3xy\cdot2x^2y\)
\(=\left(3\cdot2\right)\cdot\left(x^2\cdot x\right)\cdot\left(y\cdot y\right)\)
\(=6x^3y^2\)


ủa ,câu hỏi đâu?