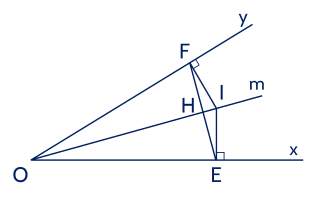
Cho $\widehat{xOy}$. Lấy các điểm $A, \, B$ thuộc tia $O x$ sao cho $O A>O B$. Lấy các điểm $C, \, D$ thuộc $O y$ sao cho $O C=O A, \, O D=O B$. Gọi $E$ là giao điểm của $A D$ và $B C$. Chứng minh rằng
a) $A D=B C$.
b) $\triangle A B E=\triangle C D E$.
c) $O E$ là tia phân giác của $\widehat{x O y}$.




a)
Xét \(\Delta AOD\) và \(\Delta COB\) có: \(\left\{{}\begin{matrix}OA=OC\left(gt\right)\\\widehat{O}:chung\\OB=OD\left(gt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AOD=\Delta COB\left(c.g.c\right)\)
\(\Rightarrow AD=BC\left(\text{2 cạnh tương ứng}\right)\left(\text{đpcm}\right)\)
b)
Nối A với C
Ta có: \(\left\{{}\begin{matrix}OA=OC\\OB=OD\end{matrix}\right.\left(gt\right)\Rightarrow OA-OB=OC-OD\)
Hay \(AB=CD\)
Xét \(\Delta ABC\) và \(\Delta CDA\) có: \(\left\{{}\begin{matrix}AB=CD\left(cmt\right)\\AC:chung\\AD=BC\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABC=\Delta DCA\left(c.c.c\right)\)
\(\Rightarrow\widehat{ABC}=\widehat{CDA}\left(\text{2 góc tương ứng}\right)\)
Vì \(\Delta AOD=\Delta COB\left(cmt\right)\Rightarrow\widehat{A}=\widehat{C}\left(\text{2 góc tương ứng}\right)\)
Xét \(\Delta ABE\) và \(\Delta CDE\) có: \(\left\{{}\begin{matrix}\widehat{ABC}=\widehat{CDA}\left(cmt\right)\\AB=CD\left(cmt\right)\\\widehat{A}=\widehat{C}\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta ABE=\Delta CDE\left(g.c.g\right)\left(\text{đpcm}\right)\)
c) Vì \(\Delta ABE=\Delta CDE\left(cmt\right)\Rightarrow AE=CE\left(\text{2 cạnh tương ứng}\right)\)
Xét \(\Delta AOE\) và \(\Delta COE\) có: \(\left\{{}\begin{matrix}OA=OC\left(gt\right)\\\widehat{A}=\widehat{C}\left(cmt\right)\\AE=CE\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta AOE=\Delta COE\left(c.g.c\right)\\ \Rightarrow\widehat{AOE}=\widehat{COE}\left(\text{2 góc tương ứng}\right)\)
`=> OE` là phân giác của \(\widehat{xOy}\) (đpcm)
em bổ sung hình nhé