Nếu a,b,c là các số thực thỏa mãn ab + bc + ca = -1, tìm giá trị nhỏ nhất của biểu thức P
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LH
1
KV
8 tháng 11 2023
Do a chia 3 dư 2 nên a = 3k + 2 (k ∈ ℕ)
⇒ a² - 1 = (3k + 2)² - 1
= (3k)² + 2.3k.2 + 2² - 1
= 9k² + 12k + 3
= 3(3k² + 4k + 1) ⋮ 3
Vậy (a² - 1) ⋮ 3
TT
0
DT
Dang Tung
CTVHS
8 tháng 11 2023
\(A=8.\left(3^2+1\right)\left(3^4+1\right)....\left(3^{16}+1\right)\\ =\left(3^2-1\right)\left(3^2+1\right)\left(3^4+1\right)....\left(3^{16}+1\right)\\ =\left(3^4-1\right)\left(3^4+1\right)....\left(3^{16}+1\right)\\ =\left(3^8-1\right)....\left(3^{16}+1\right)\\ =\left(3^{16}-1\right)\left(3^{16}+1\right)\\ =3^{32}-1\)
KV
8 tháng 11 2023
A = 8.(3² + 1)(3⁴ + 1)(3⁸ + 1)(3¹⁶ + 1)
= (3² - 1)(3² + 1)(3⁴ + 1)(3⁸ + 1)(3¹⁶ + 1)
= (3⁴ - 1)(3⁴ + 1)(3⁸ + 1)(3¹⁶ + 1)
= (3⁸ - 1)(3⁸ + 1)(3¹⁶ + 1)
= (3¹⁶ - 1)(3¹⁶ + 1)
= 3³² - 1
KV
8 tháng 11 2023
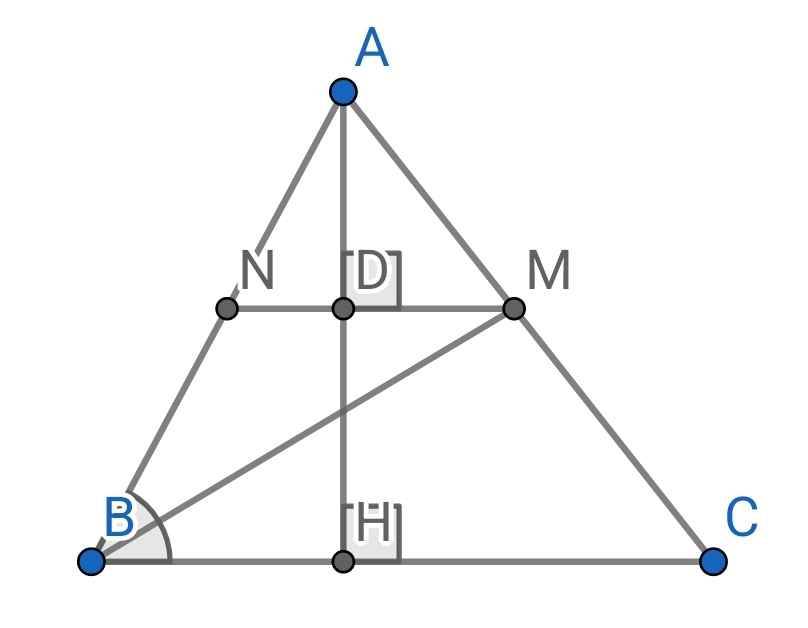a) Ta có:
AH là đường cao của ∆ABC (gt)
⇒ AH ⊥ BC
Lại có:
MN ⊥ AH (gt)
⇒ MN // BC
Tứ giác BCMN có:
MN // BC (cmt)
⇒ BCMN là hình thang
b) Do MN // BC (cmt)
⇒ ∠NMB = ∠MBC (so le trong)
Do BM là tia phân giác của ∠ABC (gt)
⇒ ∠ABM = ∠MBC
⇒ ∠NBM = ∠MBC
Mà ∠NMB = ∠MBC (cmt)
⇒ ∠NBM = ∠NMB
∆BMN có:
∠NBM = ∠NMB (cmt)
⇒ ∆BMN cân tại N
⇒ BN = MN
ND
0
Sao mình không thấy biểu thức P nhỉ?