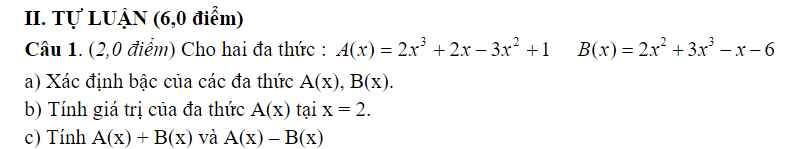 Mọi người giúp tui với nó khó quá điiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii :((
Mọi người giúp tui với nó khó quá điiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiiii :((
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔACB có AB<AC<BC
mà \(\widehat{ACB};\widehat{ABC};\widehat{BAC}\) lần lượt là góc đối diện của các cạnh AB,AC,BC
nên \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
b: E nằm trên đường trung trực của AC
=>EA=EC
=>ΔEAC cân tại E
c: Ta có: \(\widehat{EAC}+\widehat{EAB}=\widehat{BAC}=90^0\)
\(\widehat{ECA}+\widehat{EBA}=90^0\)(ΔABC vuông tại A)
mà \(\widehat{EAC}=\widehat{ECA}\)(ΔEAC cân tại E)
nên \(\widehat{EAB}=\widehat{EBA}\)
=>ΔEAB cân tại E
=>EA=EB
mà EA=EC
nên EB=EC
=>E là trung điểm của BC
Xét ΔABC có
BM,CN là các đường trung tuyến
BM cắt CN tại G
Do đó: G là trọng tâm của ΔABC
=>A,G,E thẳng hàng
a) So sánh các góc A, B, C:
Tam giác ABC là tam giác vuông tại A (vì BC2 = AB2 + AC2). Do đó ta có:
Góc A là góc vuông, có độ lớn là 90 độ.
Góc B nhỏ hơn góc C (vì cạnh đối diện góc B nhỏ hơn cạnh đối diện góc C).
b) Trung trực của AC cắt tại BC tại E chứng minh tam giác AEC cân:
Gọi D là trung điểm của AC. Khi đó, DE là trung trực của AC. Theo tính chất của trung trực, ta có BD = DC.
Do tam giác ABC là tam giác vuông tại A, nên BD = DC = \(\dfrac{1}{2}\)AC = 4cm.
Vì vậy, tam giác AEC là tam giác cân tại E (vì AE = EC).

\(B=2^{2016}-2^{2015}+...+2^2-2^1+1\)
=>\(2B=2^{2017}-2^{2016}+...+2^3-2^2+2\)
=>\(2B+B=2^{2017}-2^{2016}+...+2^3-2^2+2+2^{2016}-2^{2015}+...+2^2-2+1\)
=>\(3B=2^{2017}+1\)
=>\(B=\dfrac{2^{2017}+1}{3}\)
Lời giải:
$B=2^{2016}-2^{2015}+2^{2014}-2^{2013}+...+2^2-2^1+2^0$
$2B=2^{2017}-2^{2016}+2^{2015}-2^{2014}+...+2^3-2^2+2^1$
$\Rightarrow B+2B=2^{2017}+2^0=2^{2017}+1$
$\Rightarrow 3B=2^{2017}+1$
$\Rightarrow B=\frac{2^{2017}+1}{3}$

a: Xét ΔBAE vuông tại A và ΔBDE vuông tại D có
BE chung
BA=BD
Do đó; ΔBAE=ΔBDE
=>EA=ED
=>ΔEAD cân tại E
Ta có: BA=BD
=>B nằm trên đường trung trực của AD(1)
Ta có: EA=ED
=>E nằm trên đường trung trực củaAD(2)
Từ (1),(2) suy ra BE là đường trung trực của AD
b: Xét ΔBAD có
AH,BE là các đường cao
AH cắt BE tại I
Do đó: I là trực tâm của ΔBAD
=>DI\(\perp\)AB
mà AC\(\perp\)AB
nên DI//AC
c: Gọi K là giao điểm của CF và BA
Xét ΔBKC có
BF,CA là các đường cao
BF cắt CA tại E
Do đó: E là trực tâm của ΔBKC
=>KE\(\perp\)BC
mà ED\(\perp\)BC
và KE,ED có điểm chung là E
nên K,E,D thẳng hàng
=>BA,ED,CF đồng quy

a: Xét ΔABC có \(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^0\)
=>\(\widehat{ACB}+80^0+60^0=180^0\)
=>\(\widehat{ACB}=40^0\)
Xét ΔABC có \(\widehat{ACB}< \widehat{ABC}< \widehat{BAC}\)
mà AB,AC,BC lần lượt là cạnh đối diện của các góc ACB,ABC,BAC
nên AB<AC<BC
b: Xét ΔABE và ΔDBE có
BA=BD
\(\widehat{ABE}=\widehat{DBE}\)
BE chung
Do đó: ΔBAE=ΔBDE
d: Ta có; ΔBAE=ΔBDE
=>EA=ED
=>E nằm trên đường trung trực của AD(1)
Ta có: BA=BD
=>B nằm trên đường trung trực của AD(2)
Từ (1),(2) suy ra BE là đường trung trực của AD
=>BE\(\perp\)AD tại trung điểm của AD
=>H là trung điểm của AD

\(\dfrac{x+1}{3}=\dfrac{y-2}{4}=\dfrac{z-1}{13}\)
=>\(\dfrac{2x+2}{6}=\dfrac{3y-6}{12}=\dfrac{z-1}{13}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{2x+2}{6}=\dfrac{3y-6}{12}=\dfrac{z-1}{13}=\dfrac{2x-3y+z+2+6-1}{6-12+13}=\dfrac{49}{7}=7\)
=>\(\dfrac{x+1}{3}=\dfrac{y-2}{4}=\dfrac{z-1}{13}=7\)
=>\(x+1=21;y-2=28;z-1=91\)
=>x=20; y=30; z=92
Lời giải:
Áp dụng TCDTSBN:
$\frac{x+1}{3}=\frac{y-2}{4}=\frac{z-1}{13}$
$=\frac{2(x+1)}{6}=\frac{3(y-2)}{12}=\frac{z-1}{13}$
$=\frac{2(x+1)-3(y-2)+(z-1)}{6-12+13}=\frac{2x-3y+z+7}{7}=\frac{42+7}{7}=7$
$\Rightarrow x+1=3.7=21; y-2=4.7=28; z-1=13.7=91$
$\Rightarrow x=20; y=30; z=92$

a: \(M\left(x\right)=5-8x^4+2x^3+x+\left(5x^2+1\right)x^2-4x^3\)
\(=5-8x^4+\left(2x^3-4x^3\right)+x+5x^4+x^2\)
\(=-3x^4-2x^3+x^2+x+5\)
\(N\left(x\right)=x\left(3x^4+x^3-4\right)-\left(4x^3-7+2x^4+3x^5\right)\)
\(=3x^5+x^4-4x-4x^3+7-2x^4-3x^5\)
\(=-x^4-4x^3-4x+7\)
b: P(x)=M(x)+N(x)
\(=-3x^4-2x^3+x^2+x+5-x^4-4x^3-4x+7\)
\(=-4x^4-6x^3+x^2-3x+12\)
Q(x)=M(x)-N(x)
\(=-3x^4-2x^3+x^2+x+5+x^4+4x^3+4x-7\)
\(=-2x^4+2x^3+x^2+5x-2\)
c: \(P\left(1\right)=-4\cdot1^4-6\cdot1^3+1^2-3\cdot1+12\)
=-4-6+1-3+12
=-10-2+12
=0
=>x=1 là nghiệm của P(x)
\(Q\left(1\right)=-2\cdot1^4+2\cdot1^3+1^2+5\cdot1-2\)
=-2+2+1+5-2
=4
=>x=1 không là nghiệm của P(x)
d: \(F\left(x\right)=Q\left(x\right)-\left(-2x^4+2x^3+x^2-12\right)\)
\(=-2x^4+2x^3+x^2+5x-2+2x^4-2x^3-x^2+12\)
=5x+10
Đặt F(x)=0
=>5x+10=0
=>5x=-10
=>x=-2

a: Xét ΔAEB và ΔADC có
AE=AD
\(\widehat{BAE}\) chung
AB=AC
Do đó: ΔAEB=ΔADC
=>EB=DC
b: Ta có: AD+DB=AB
AE+EC=AC
mà AD=AE và AB=AC
nên DB=EC
Xét ΔDBC và ΔECB có
DB=EC
\(\widehat{DBC}=\widehat{ECB}\)
BC chung
Do đó: ΔDBC=ΔECB
=>\(\widehat{DCB}=\widehat{EBC}\)
=>\(\widehat{KBC}=\widehat{KCB}\)
=>KB=KC
Xét ΔABK và ΔACK có
AB=AC
BK=CK
AK chung
Do đó: ΔABK=ΔACK
=>\(\widehat{BAK}=\widehat{CAK}\)
=>AK là phân giác của góc BAC
c: Xét ΔKDB và ΔKEC có
KB=KC
\(\widehat{KBD}=\widehat{KCE}\)
BD=CE
Do đó; ΔKDB=ΔKEC
d: Ta có: AB=AC
=>A nằm trên đường trung trực củaBC(1)
Ta có: KB=KC
=>K nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra AK là đường trung trực của BC
=>AK\(\perp\)BC tại I

\(\dfrac{3x^6-4x^4}{x^3}-\dfrac{3x^7}{x^4}+1=0\)
=>\(3x^3-4x-3x^3+1=0\)
=>-4x+1=0
=>-4x=-1
=>\(x=\dfrac{1}{4}\)
`#3107.101107`
`1.`
`a)`
`A(x) = 2x^3 - 3x^2 + 2x + 1`
Bậc của đa thức: `3`
`B(x) = 3x^3 + 2x^2 - x - 6`
Bậc của đa thức: `3`
`b)`
Thay `x = 2` vào A:
`A(2) = 2 * 2^3 - 3 * 2^2 + 2 * 2 + 1`
`= 2^4 - 3 * 4 + 2^2 + 1`
`= 16 - 12 + 4 + 1 = 9`
Vậy, tại `x = 2` thì `A(2) = 9`
`c)`
`A(x) + B(x)`
`= 2x^3 - 3x^2 + 2x + 1 + 3x^3 + 2x^2 - x - 6`
`= (2x^3 + 3x^3) + (-3x^2 + 2x^2) + (2x - x) + (1 - 6)`
`= 5x^3 - x^2 + x - 5`
`A(x) - B(x)`
`= 2x^3 - 3x^2 + 2x + 1 - (3x^3 + 2x^2 - x - 6)`
`= 2x^3 - 3x^2 + 2x + 1 - 3x^3 - 2x^2 + x + 6`
`= (2x^3 - 3x^3) - (3x^2 + 2x^2) + (2x + x) + (1 + 6)`
`= -x^3 - 5x^2 + 3x + 7.`