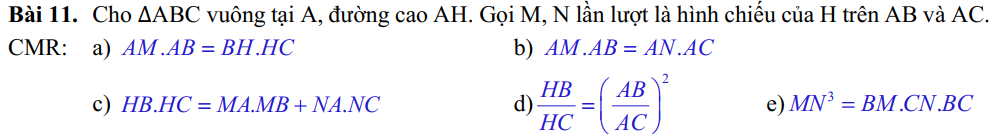 chỉ cách làm câu d và e
chỉ cách làm câu d và e
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



42 told off
43 brought up
44 looked up
45 get on
46 fell for
47 falling out
48 gotten over

1. Look! The car is moving so fast.
2. Listen! Someone is whispering in the next room.
3. Is your friend sitting next to the beautiful girl over there at present?
4. Now Joy is trying to pass the examination.
5. It’s 11 o’clock, and my mom is cooking lunch in the kitchen.
6. Keep silent! You are singing so loudly.
7. I am not staying at home at present.
8. Now Hana is lying to her mother about her bad marks.
9. At present they are traveling to LA.
10. Jim is not working in his office now.
\(#FallenAngel\)

6h40p=20/3 giờ
Gọi thời gian làm riêng hoàn thành công việc của người thứ nhất và người thứ hai lần lượt là a(giờ) và b(giờ)
(Điều kiện: a>0; b>0)
Trong 1 giờ, người thứ nhất làm được: \(\dfrac{1}{a}\)(công việc)
Trong 1 giờ, người thứ hai làm được: \(\dfrac{1}{b}\)(công việc)
Trong 1 giờ, hai người làm được: \(1:\dfrac{20}{3}=\dfrac{3}{20}\)(công việc)
Do đó, ta có: \(\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{3}{20}\left(1\right)\)
Trong 5 giờ, người thứ nhất làm được: \(\dfrac{5}{a}\)(công việc)
Trong 8 giờ, người thứ hai làm được: \(\dfrac{8}{b}\)(công việc)
Nếu người thứ nhất làm trong 5 giờ, sau đó nghỉ và người thứ hai làm trong 8 giờ thì xong nên ta có: \(\dfrac{5}{a}+\dfrac{8}{b}=1\left(2\right)\)
Từ (1),(2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{3}{20}\\\dfrac{5}{a}+\dfrac{8}{b}=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{5}{a}+\dfrac{5}{b}=\dfrac{3}{4}\\\dfrac{5}{a}+\dfrac{8}{b}=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{5}{a}+\dfrac{8}{b}-\dfrac{5}{a}-\dfrac{5}{b}=1-\dfrac{3}{4}\\\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{3}{20}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{3}{b}=\dfrac{1}{4}\\\dfrac{1}{a}=\dfrac{3}{20}-\dfrac{1}{b}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}b=12\\\dfrac{1}{a}=\dfrac{3}{20}-\dfrac{1}{12}=\dfrac{9}{60}-\dfrac{5}{60}=\dfrac{4}{60}=\dfrac{1}{15}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}b=12\\a=15\end{matrix}\right.\left(nhận\right)\)
Vậy: thời gian làm riêng hoàn thành công việc của người thứ nhất và người thứ hai lần lượt là 15(giờ) và 12(giờ)
Gọi thời gian nếu làm riêng của người thứ nhất, người thứ hai để hoàn thành công việc lần lượt là $a,b$ (giờ; $a,b>0$)
Mỗi giờ người thứ nhất làm được: $\frac1a$ (công việc)
Mỗi giờ người thứ hai làm được: $\frac1b$ (công việc)
Vì hai người cùng làm việc thì trong 6 giờ 40 phút (= $\frac{20}{3}$ giờ) thì xong công việc nên ta có phương trình: $\frac{20}{3}(\frac 1a+\frac1b)=1$
$\Leftrightarrow \frac1a+\frac1b=\frac{3}{20}$ (1)
Vì nếu người thứ nhất làm riêng trong 5 giờ rồi người thứ hai tiếp tục làm nốt trong 8 giờ thì xong công việc nên ta có phương trình:
$\frac5a+\frac8b=1$ (2)
Từ (1) và (2) ta có hệ: $\begin{cases} \frac1a+\frac1b=\frac{3}{20} \\ \frac5a+\frac8b=1 \end{cases}$
Đặt $\frac 1a=u:\frac1b=v;(u,v>0)$
Khi đó hot trở thành: $\begin{cases} u+v=\frac{3}{20}\\ 5u+8v=1\end{cases} \Leftrightarrow \begin{cases} u=\frac{1}{15}\\v=\frac{1}{12}\end{cases}$
$\Rightarrow \begin{cases} \frac1a=\frac{1}{15}\\\frac1b=\frac{1}{12} \end{cases} \Rightarrow \begin{cases} a=15 (tm)\\b=12(tm) \end{cases}$
Vậy: ...
#$\mathtt{Toru}$


Gọi đường thẳng (d): y=ax+b(a\(\ne\)0) là đường thẳng đi qua hai điểm (2;0); (-1;-2)
Thay x=2 và y=0 vào (d), ta được:
\(a\cdot2+b=0\)(1)
Thay x=-1 và y=-2 vào (d), ta được:
\(a\cdot\left(-1\right)+b=-2\left(2\right)\)
Từ (1),(2) ta có hệ phương trình: \(\left\{{}\begin{matrix}2a+b=0\\-a+b=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2a+b+a-b=0-\left(-2\right)\\b=-2a\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3a=2\\b=-2a\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=\dfrac{2}{3}\\b=-2\cdot\dfrac{2}{3}=-\dfrac{4}{3}\end{matrix}\right.\)
Vậy: (d): \(y=\dfrac{2}{3}x-\dfrac{4}{3}\)
=>\(\dfrac{2}{3}x-y=\dfrac{4}{3}\)

ĐKXĐ: \(x\notin\left\{1;-1;2;-2\right\}\)
\(\dfrac{x+4}{x-1}+\dfrac{x-4}{x+1}=\dfrac{x+8}{x-2}+\dfrac{x-8}{x+2}+6\)
=>\(\dfrac{\left(x+4\right)\left(x+1\right)+\left(x-4\right)\left(x-1\right)}{\left(x-1\right)\left(x+1\right)}=\dfrac{\left(x+8\right)\left(x+2\right)+\left(x-8\right)\left(x+2\right)+6\left(x-2\right)\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}\)
=>\(\dfrac{2x^2+8}{x^2-1}=\dfrac{x^2+10x+16+x^2-10x+16+6\left(x^2-4\right)}{x^2-4}\)
=>\(\dfrac{2x^2+8}{x^2-1}=\dfrac{2x^2+32+6x^2-24}{x^2-4}\)
=>\(\dfrac{2x^2+8}{x^2-1}=\dfrac{8x^2+8}{x^2-4}\)
=>\(\dfrac{x^2+4}{x^2-1}=\dfrac{4\left(x^2+1\right)}{x^2-4}\)
=>\(4\left(x^2+1\right)\left(x^2-1\right)=\left(x^2+4\right)\left(x^2-4\right)\)
=>\(4\left(x^4-1\right)=x^4-16\)
=>\(4x^4-4-x^4+16=0\)
=>\(3x^4+12=0\)(vô lý)
Vậy: Phương trình vô nghiệm

\(n_{Cu}=\dfrac{32}{64}=0,5\left(mol\right)\)
\(n_{AgNO_3}=2.0,16=0,32\left(mol\right)\)
PTHH:
\(Cu+2AgNO_3\rightarrow Cu\left(NO_3\right)_2+2Ag\)
0,125 0,25 0,125 0,25
Số mol Cu phản ứng :
\(n_{Cu\left(pư\right)}=\dfrac{51-32}{2.108-64}=0,125\left(mol\right)\)
a,\(C_{M\left(Cu\left(NO_3\right)_2\right)}=\dfrac{0,125}{2}=\dfrac{1}{16}\left(M\right)\)
\(C_{M\left(AgNO_3dư\right)}=\dfrac{0,32-0,25}{2}=\dfrac{7}{200}\left(M\right)\)
Câu b để mình suy nghĩ sau:)

Bài 1:
e: ĐKXĐ: \(x\notin\left\{1;-1\right\}\)
\(\dfrac{x+1}{x-1}-\dfrac{x-1}{x+1}=\dfrac{16}{x^2-1}\)
=>\(\dfrac{\left(x+1\right)^2-\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}=\dfrac{16}{\left(x-1\right)\left(x+1\right)}\)
=>\(\left(x+1\right)^2-\left(x-1\right)^2=16\)
=>\(\left(x+1+x-1\right)\left(x+1-x+1\right)=16\)
=>4x=16
=>x=4(nhận)
f: ĐKXĐ: \(x\notin\left\{1-1\right\}\)
\(\left(1-\dfrac{x-1}{x+1}\right)\left(x+2\right)=\dfrac{x+1}{x-1}+\dfrac{x-1}{x+1}\)
=>\(\dfrac{x+1-x+1}{\left(x+1\right)}\left(x+2\right)=\dfrac{\left(x+1\right)^2+\left(x-1\right)^2}{\left(x-1\right)\left(x+1\right)}\)
=>\(\dfrac{2\left(x+2\right)\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}=\dfrac{2x^2+2}{\left(x-1\right)\left(x+1\right)}\)
=>\(2\left(x+2\right)\left(x-1\right)=2\left(x^2+1\right)\)
=>\(\left(x+2\right)\left(x-1\right)=x^2+1\)
=>\(x^2+x-2=x^2+1\)
=>x-2=1
=>x=3(nhận)
a: ĐKXĐ: \(x\notin\left\{0;-1;4\right\}\)
\(\dfrac{11}{x}=\dfrac{9}{x+1}+\dfrac{2}{x-4}\)
=>\(\dfrac{11}{x}=\dfrac{9\left(x-4\right)+2\left(x+1\right)}{\left(x+1\right)\left(x-4\right)}\)
=>\(\dfrac{11}{x}=\dfrac{11x-34}{x^2-3x-4}\)
=>\(11\left(x^2-3x-4\right)=x\left(11x-34\right)\)
=>\(11x^2-33x-44=11x^2-34x\)
=>-33x-44=-34x
=>-33x+34x=44
=>x=44(nhận)
b: ĐKXĐ: \(x\ne4\)
\(\dfrac{14}{3x-12}-\dfrac{2+x}{x-4}=\dfrac{3}{8-2x}-\dfrac{5}{6}\)
=>\(\dfrac{14}{3\left(x-4\right)}-\dfrac{x+2}{x-4}=\dfrac{-3}{2\left(x-4\right)}-\dfrac{5}{6}\)
=>\(\dfrac{28}{6\left(x-4\right)}-\dfrac{6\left(x+2\right)}{6\left(x-4\right)}=\dfrac{-9}{6\left(x-4\right)}-\dfrac{5\left(x-4\right)}{6\left(x-4\right)}\)
=>28-6(x+2)=-9-5(x-4)
=>28-6x-12=-9-5x+20
=>-6x+16=-5x+11
=>-6x+5x=11-16
=>-x=-5
=>x=5(nhận)
c: ĐKXĐ: \(x\notin\left\{\dfrac{1}{3};-\dfrac{1}{3}\right\}\)
\(\dfrac{12}{1-9x^2}=\dfrac{1-3x}{1+3x}-\dfrac{1+3x}{1-3x}\)
=>\(\dfrac{12}{\left(1-3x\right)\left(1+3x\right)}=\dfrac{\left(1-3x\right)^2-\left(1+3x\right)^2}{\left(1+3x\right)\left(1-3x\right)}\)
=>\(\left(1-3x\right)^2-\left(1+3x\right)^2=12\)
=>\(9x^2-6x+1-9x^2-6x-1=12\)
=>-12x=12
=>x=-1(nhận)
d: ĐKXĐ: \(x\notin\left\{0;5;-5\right\}\)
\(\dfrac{x+5}{x^2-5x}-\dfrac{x+25}{2x^2-50}=\dfrac{x-5}{2x^2+10x}\)
=>\(\dfrac{x+5}{x\left(x-5\right)}-\dfrac{x+25}{2\left(x-5\right)\left(x+5\right)}=\dfrac{x-5}{2x\left(x+5\right)}\)
=>\(\dfrac{2\left(x+5\right)^2}{2x\left(x-5\right)\left(x+5\right)}-\dfrac{x\left(x+25\right)}{2x\left(x-5\right)\left(x+5\right)}=\dfrac{\left(x-5\right)^2}{2x\left(x+5\right)\left(x-5\right)}\)
=>\(2\left(x+5\right)^2-x\left(x+25\right)=\left(x-5\right)^2\)
=>\(2x^2+20x+50-x^2-25x=x^2-10x+25\)
=>-5x+50=-10x+25
=>5x=-25
=>x=-5(loại)
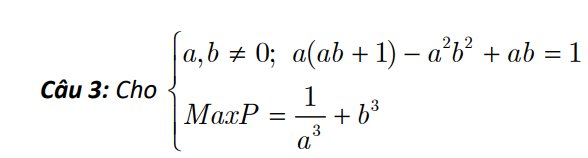



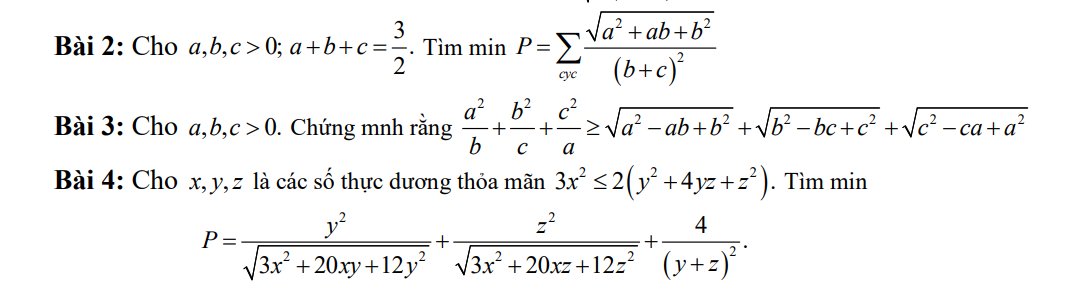
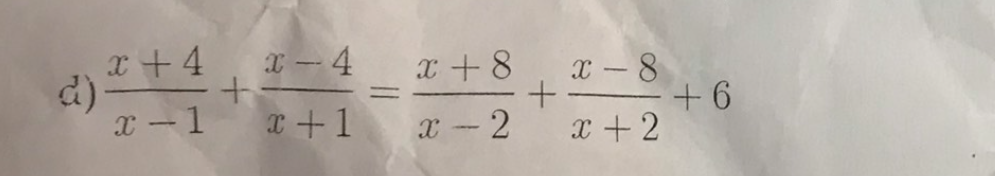

a: Xét ΔAHB vuông tại H có HM là đường cao
nên \(AM\cdot AB=AH^2\left(1\right)\) và \(MA\cdot MB=HM^2\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right);NA\cdot NC=NH^2\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\left(3\right);AB^2=BH\cdot BC;AC^2=CH\cdot BC\)
Từ (1) và (3) suy ra \(AM\cdot AB=HB\cdot HC\)
b: Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
c: Xét tứ giác AMHN có \(\widehat{AMH}=\widehat{ANH}=\widehat{MAN}=90^0\)
nên AMHN là hình chữ nhật
=>\(HA^2=HM^2+HN^2\)
=>\(HB\cdot HC=MA\cdot MB+NA\cdot NC\)
d: \(\dfrac{AB^2}{AC^2}=\dfrac{BH\cdot BC}{CH\cdot BC}=\dfrac{BH}{CH}\)
=>\(\dfrac{HB}{HC}=\left(\dfrac{AB}{AC}\right)^2\)
e: Xét ΔAHB vuông tại H có HM là đường cao
nên \(BM\cdot BA=BH^2\)
=>\(BM=\dfrac{BH^2}{BA}\)
Xét ΔAHC vuông tại H có HN là đường cao
nên \(CN\cdot CA=CH^2\)
=>\(CN=\dfrac{CH^2}{CA}\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH\cdot BC=AB\cdot AC\)
=>\(BC=\dfrac{AB\cdot AC}{AH}\)
\(BM\cdot CN\cdot BC=\dfrac{BH^2}{BA}\cdot\dfrac{CH^2}{CA}\cdot\dfrac{AB\cdot AC}{AH}\)
\(=\dfrac{BH^2}{AH}\cdot CH^2=\dfrac{\left(BH\cdot CH\right)^2}{AH}=\dfrac{AH^4}{AH}=AH^3\)
mà AH=MN(AMHN là hình chữ nhật)
nên \(BM\cdot CN\cdot BC=MN^3\)