mik bít cách

A B C H D 12 16

Xét tam giác ABC vuông tại A, đường cao AH

Áp dụng định lí Pytago cho tam giác ABC vuông tại A 

\(BC^2=AB^2+AC^2=144+256=400\Rightarrow BC=20\)cm 

* Áp dụng hệ thức : \(AB^2=BH.BC\Rightarrow BH=\frac{AB^2}{BC}=\frac{144}{20}=\frac{36}{5}\)cm 

\(\Rightarrow HC=BC-HB=20-\frac{36}{5}=\frac{64}{5}\)cm 

Vì AD là phân giác nên : \(\frac{AB}{AC}=\frac{BD}{DC}\Rightarrow\frac{DC}{AC}=\frac{BD}{AB}\)

Áp dụng tính chất dãy tỉ số bằng nhau 

\(\frac{DC}{AC}=\frac{BD}{AB}=\frac{DC+BD}{AC+AB}=\frac{20}{12+16}=\frac{20}{28}=\frac{5}{7}\)

\(\Rightarrow BD=\frac{5}{7}AB=\frac{5}{7}.12=\frac{60}{7}\)cm 

\(\Rightarrow HD=BD-BH=\frac{60}{7}-\frac{36}{5}=\frac{48}{35}\)cm 

* Áp dụng hệ thức : \(AH.BC=AB.AC\Rightarrow AH=\frac{AB.AC}{BC}=\frac{192}{20}=\frac{48}{5}\)cm 

Áp dụng định lí Pytago cho tam giác AHD vuông tại H 

\(AD^2=AH^2+HD^2=\left(\frac{48}{5}\right)^2+\left(\frac{48}{35}\right)^2=\frac{4608}{49}\Rightarrow AD=\frac{48\sqrt{2}}{7}\)cm 

a,\(P=1-\left(\frac{a-\sqrt{a}}{\sqrt{a}-1}\right)^2=1-\left(\frac{\sqrt{a}\left(\sqrt{a}-1\right)}{\sqrt{a-1}}\right)^2=1-a\)(đk : tự tìm nhé )

b, \(1-a=\sqrt{a}< =>a+\sqrt{a}-1=0\)

\(< =>4a+4\sqrt{a}+1-5=0\)

\(< =>\left(2\sqrt{a}+1\right)^2-\sqrt{5}^2=0\)

\(< =>\left(2\sqrt{a}+1-\sqrt{5}\right)\left(2\sqrt{a}+1+\sqrt{5}\right)=0\)

<=> ...

\(P=1-\frac{a-\sqrt{a}}{\sqrt{a}-1}+\frac{a+\sqrt{a}}{\sqrt{a}+1}-\frac{\left(a+\sqrt{a}\right)\left(a-\sqrt{a}\right)}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}\)

\(=1-\sqrt{a}+\sqrt{a}-\frac{\sqrt{a}.\left(\sqrt{a}+1\right).\sqrt{a}.\left(\sqrt{a}-1\right)}{\left(\sqrt{a}+1\right)\left(\sqrt{a}-1\right)}=1-a\)

câu b thì giống câu lúc nãy mình làm 

Giả sử \(a=\sqrt{3}+\sqrt{5}\inℚ\)

\(\Rightarrow a^2=3+2\sqrt{3}.\sqrt{5}+5\inℚ\)

\(\Rightarrow a^2-8=2\sqrt{15}\inℚ\)

Vô lý do \(a^2-8\inℚ;2\sqrt{15}\in I\)

Do đó \(\sqrt{3}+\sqrt{5}\)là số vô tỷ.

sửa đề : \(\sqrt{27+10\sqrt{2}}-\sqrt{18+8\sqrt{2}}\)

\(=\sqrt{5^2+2.5\sqrt{2}+2}-\sqrt{4^2+2.4\sqrt{2}+2}\)

\(=\sqrt{\left(5+\sqrt{2}\right)^2}-\sqrt{\left(4+\sqrt{2}\right)^2}=\left|5+\sqrt{2}\right|-\left|4+\sqrt{2}\right|\)

\(=5+\sqrt{2}-4-\sqrt{2}=1\)

=1 nha

t.i.c.k mình nha

bạn nào 10sp gúp mình đi

Là thế lào

Mọi người làm hết giúp mình với

Trả lời :

My family often sex together

:)

~~Học Dốt~~

Ta có: A = \(\frac{\sqrt{5}+3}{\sqrt{2}+\sqrt{3+\sqrt{5}}}+\frac{3-\sqrt{5}}{\sqrt{2}-\sqrt{3-\sqrt{5}}}\) 

\(=\frac{\sqrt{10}+3\sqrt{2}}{2+\sqrt{6+2\sqrt{5}}}+\frac{3\sqrt{2}-\sqrt{10}}{2-\sqrt{3-\sqrt{5}}}\) 

\(=\frac{\sqrt{10}+3\sqrt{2}}{2+\left(1+\sqrt{5}\right)}+\frac{3\sqrt{2}-\sqrt{10}}{2-\left(\sqrt{5}-1\right)}\) 

\(=\sqrt{2}+\sqrt{2}\) 

\(=2\sqrt{2}\)

f(x1)=3x1f(x1)=3x1

f(x2)=3x2f(x2)=3x2

Theo giả thiết, ta có:

x1<x2⇔3.x1<3.x2x1<x2⇔3.x1<3.x2 ( vì 3>03>0 nên chiều bất đẳng thức không đổi)

⇔f(x1)<f(x2)⇔f(x1)<f(x2) (vì f(x1)=3x1;f(x1)=3x1;f(x2)=3x2)f(x2)=3x2)

Vậy với x1<x2x1<x2 ta được f(x1)<f(x2)f(x1)<f(x2) nên hàm số y=3xy=3x đồng biến trên RR. 

Chú ý:

Ta cũng có thể làm như sau:

Vì x1<x2x1<x2 nên x1−x2<0x1−x2<0

Từ đó: f(x1)−f(x2)=3x1−3x2=3(x1−x2)<0f(x1)−f(x2)=3x1−3x2=3(x1−x2)<0 

Hay f(x1)<f(x2)f(x1)<f(x2) 

Vậy với x1<x2x1<x2 ta được f(x1)<f(x2)f(x1)<f(x2) nên hàm số y=3xy=3x đồng biến trên R

Do \(x_1< x_2\Rightarrow3x_1< 3x_2\)

\(\Rightarrow f\left(x_1\right)< f\left(x_2\right)\)

Hàm số \(f\)đồng biến trên \(ℝ\)khi :

\(\forall x_1,x_2\inℝ\): \(x_1< x_2\Rightarrow f\left(x_1\right)< f\left(x_2\right)\)

=> Hàm số đã cho đồng biến trên \(ℝ\)

+) Thay giá trị của xx vào biểu thức của hàm số y=0,5xy=0,5x, ta được:

f(−2,5)=0,5.(−2,5)=−1,25f(−2,5)=0,5.(−2,5)=−1,25.

 f(−2,25)=0,5.(−2,25)=−1,125f(−2,25)=0,5.(−2,25)=−1,125.

f(−1,5)=0,5.(−1,5)=−0,75f(−1,5)=0,5.(−1,5)=−0,75.

f(−1)=0,5.(−1)=−0,5f(−1)=0,5.(−1)=−0,5.

f(0)=0,5.0=0f(0)=0,5.0=0.

f(1)=0,5.1=0,5f(1)=0,5.1=0,5.

f(1,5)=0,5.1,5=0,75f(1,5)=0,5.1,5=0,75.

f(2,2,5)=0,5.2,25=1,125f(2,2,5)=0,5.2,25=1,125.

f(2,5)=0,5.2,5=1,25f(2,5)=0,5.2,5=1,25.

+) Thay giá trị của xx vào biểu thức của hàm số y=0,5x+2y=0,5x+2, ta được:

f(−2,5)=0,5.(−2,5)+2=−1,25+2=0,75f(−2,5)=0,5.(−2,5)+2=−1,25+2=0,75.

f(−2,25)=0,5.(−2,25)+2=−1,125+2=0,875f(−2,25)=0,5.(−2,25)+2=−1,125+2=0,875.

f(−1,5)=0,5.(−1,5)+2=−0,75+2=1,25f(−1,5)=0,5.(−1,5)+2=−0,75+2=1,25.

f(−1)=0,5.(−1)+2=−0,5+2=1,5f(−1)=0,5.(−1)+2=−0,5+2=1,5.

f(0)=0,5.0+2=0+2=2f(0)=0,5.0+2=0+2=2.

f(1)=0,5.1+2=0,5+2=2,5f(1)=0,5.1+2=0,5+2=2,5.

f(1,5)=0,5.1,5+2=0,75+2=2,75f(1,5)=0,5.1,5+2=0,75+2=2,75.

f(2,2,5)=0,5.2,25+2=1,125+2=3,125f(2,2,5)=0,5.2,25+2=1,125+2=3,125.

f(2,5)=0,5.2,5+2=1,25+2=3,25f(2,5)=0,5.2,5+2=1,25+2=3,25.

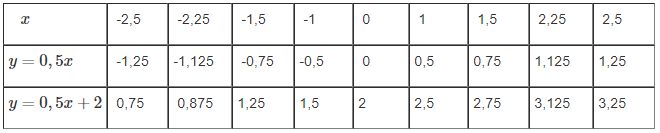
Vậy ta có bảng sau:

b)

Khi xx lấy cùng một giá trị của xx thì giá trị của hàm số y=0,5x+2y=0,5x+2 lớn hơn giá trị của hàm số y=0,5xy=0,5x là 22 đơn vị.

a)

b) Với các giá trị biến x như nhau thì hàm số y=0,5x+2 luôn lớn hơn hàm số y=0,5x hai đơn vị

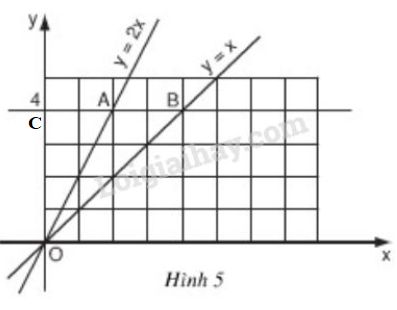
a) Xem hình trên và vẽ lại 

b)

+) Ta coi mỗi ô vuông trên hình 55 là một hình vuông có cạnh là 1cm1cm.

    Từ hình vẽ ta xác định được: A(2;4), B(4;4)A(2;4), B(4;4).

+) Tính độ dài các cạnh của ΔOAB∆OAB:

Dễ thấy AB=4−2=2AB=4−2=2  (cm)(cm).

Gọi CC là điểm biểu diễn số 44 trên trục tung, ta có OC=4cm,AC=2cm;BC=4cmOC=4cm,AC=2cm;BC=4cm

Áp dụng định lý Py-ta-go cho các tam giác vuông OACOAC và OBCOBC, ta có:

OA=√AC2+OC2=√22+42=2√5(cm)OB=√BC2+OC2=√42+42=4√2(cm)OA=AC2+OC2=22+42=25(cm)OB=BC2+OC2=42+42=42(cm)

⇒⇒ Chu vi ΔOABΔOAB là:

CΔOAB=OA+OB+ABCΔOAB=OA+OB+AB

              =2+2√5+4√2≈12,13(cm)=2+25+42≈12,13(cm)

+) Tính diện tích ΔOAB∆OAB:

Cách 1:

SΔOAB=SΔOBC−SΔOAC=1/2OC.BC−1/2OC.AC=1/2.42−1/2.4.2=8−4=4(cm2)SΔOAB=SΔOBC−SΔOAC=1/2OC.BC−1/2OC.AC=1/2.42−1/2.4.2=8−4=4(cm2)

Cách 2: 

ΔOAB có đường cao ứng với cạnh AB là OC.

⇒SΔOAB=1/2.OC.AB=1/2.4.2=4⇒S∆OAB=1/2.OC.AB=1/2.4.2=4 (cm2)

a,

b,

Từ hình vẽ ta có: yA = yB = 4 suy ra:.

    + Hoành độ của A: 4 = 2.xA => xA = 2 (*)

    + Hoành độ của B: 4 = xB => xB = 4

=> Tọa độ 2 điểm là: A(2, 4); B(4, 4)

- Tìm độ dài các cạnh của ΔOAB

- Tìm độ dài các cạnh của ΔOAB