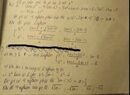cho tam giác ABC cân tại A, D là trung điểm của BC, E nằm trên đường thẳng BC, O là tâm đường tròn ngoại tiếp tam giác ABE. Đường thẳng \(\Delta1\)qua D vuông góc với OD. Đường thẳng \(\Delta2\)qua F vuông góc với AC. Đường thẳng \(\Delta3\)qua C song song với AB. Chứng minh rằng: \(\Delta1,\Delta2,\Delta3\)đồng quy.

Chứng minh bất đẳng thức: \(a^2+b^2+c^2\ge2\left(ab+bc-ac\right)\).

Cho phương trình \(x^4-\left(3m+1\right)x^2+6m-2=0.\)

Tìm tất cả các giá trị của tham số m để phương trình có 4 nghiệm phân biệt \(x_1;x_2;x_3;x_4\)sao cho \(x_1-x_2=x_2-x_3=x_3-x_4\)

vẽ đồ thị hàm số \(y=f\left(x\right)=\left|x^2-2x-3\right|\). từ đó suy ra tất cả các giá trị của tham số của m để phương trình \(\left|x^2-2x-3\right|=m^4-2m^2+4\) có 4 nghiệm phân biệt

cho tam giác abc đường cao ah đường tròn nội tiếp tâm I tiếp xúc với BC tại D, E là trung điểm của AH gọi ED cắt (I) tại F chứng minh FD là tia phân giác của BFC

Giải phương trình (x-3)căn(1+x)-x căn(4-x)=2x^2-6x-3 

\(|3x^2+2x|=|x^2+4|\)  gải hộ mình vs

Với mọi số a,b,c > 0. Chứng minh :\(\frac{a^5}{b^2}+\frac{b^5}{c^2}+\frac{c^5}{a^2}\ge a^3+b^3+c^3\)