Câu 37. Bác Đô dự định trồng ngô và đậu xanh trên một mảnh đất có diện tích $8$ ha. Nếu trồng $1$ ha ngô thì cần $20$ ngày công và thu được $40$ triệu đồng. Nếu trồng $1$ ha đậu xanh thì cần $30$ ngày công và thu được $50$ triệu đồng. Bác Đô cần trồng bao nhiêu hecta cho mỗi loại cây để thu được nhiều tiền nhất? Biết rằng, bác Đô chỉ có thể sử dụng không quá $180$ ngày công cho việc trồng ngô và đậu xanh.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có \(\overrightarrow{CM}.\overrightarrow{CB}=\overrightarrow{CM}^2\) \(\Leftrightarrow\overrightarrow{CM}.\overrightarrow{CB}-\overrightarrow{CM}^2=0\) \(\Leftrightarrow\overrightarrow{CM}\left(\overrightarrow{CB}-\overrightarrow{CM}\right)=0\) \(\Leftrightarrow\overrightarrow{CM}.\overrightarrow{MB}=\overrightarrow{0}\) \(\Leftrightarrow\) \(\overrightarrow{CM}\perp\overrightarrow{MB}\)
Như vậy những điểm M thỏa mãn \(\widehat{CMB}=90^o\) chính là những điểm thỏa mãn yêu cầu bài toán. Nói cách khác, tập hợp điểm M thỏa mãn đề bài là đường tròn đường kính BC.

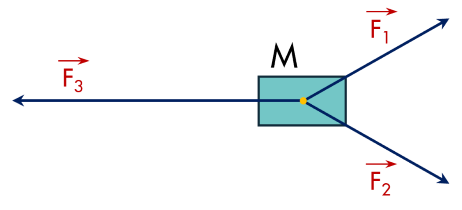
vật MM đứng yên ⇔−→F1+−→F2+−→F3=→0⇔F1→+F2→+F3→=0→
Hay −−→MA+−−→MB+−−→MC=→0MA→+MB→+MC→=0→
Gọi II là trung điểm của ABAB ⇒2−−→MI+−−→MC=→0⇒2MI→+MC→=0→⇔−−→MC=−2−−→MI⇒MC=2MI⇔MC→=−2MI→⇒MC=2MI
Gọi II là trung điểm của AB.AB.
Vì MABMAB là tam giác đều nên MI=MA.√32=25√3.MI=MA.32=503.
Vậy MC=2MI=50√3NMC=2MI=1003N
Vậy: −→F3F3→ có cường độ 50√3N1003N.

bằng 87326894586419483726264927837475758689798085740293746563739203857567389725869916490572496217946 bn nhé


\(BC:x+3y+1=0\)
\(\overrightarrow{n_{BC}}=\left(1,3\right)\Rightarrow\overrightarrow{u_{BC}}=\left(-3,1\right)\)
Phương trình đường cao \(AH\)có dạng: \(-3x+y+c=0\)
\(AH\)đi qua \(A\left(4,3\right)\Rightarrow AH:-3x+y+9=0\)
Gọi giao điểm của đường thẳng \(d\)với hai tia \(Ox,Oy\)lần lượt là \(\left(m,0\right),\left(n,0\right)\)(\(m,n>0\))
suy ra \(d:\frac{x}{m}+\frac{y}{n}=1\)
Mà \(d\)đi qua \(A\left(4,3\right)\)nên \(\frac{4}{m}+\frac{3}{n}=1\)
\(S_{OMN}=\frac{mn}{2}\)
Ta cần tìm giá trị nhỏ nhất của \(mn\)với \(\frac{4}{m}+\frac{3}{n}=1\)và \(m,n>0\).
Ta có: \(1=\frac{4}{x}+\frac{3}{y}\ge2\sqrt{\frac{12}{xy}}\Rightarrow xy\ge4.12=48\)
Dấu \(=\)xảy ra khi \(m=8,n=6\).
Vậy \(d:\frac{x}{8}+\frac{y}{6}=1\)là đường thẳng thỏa mãn ycbt.

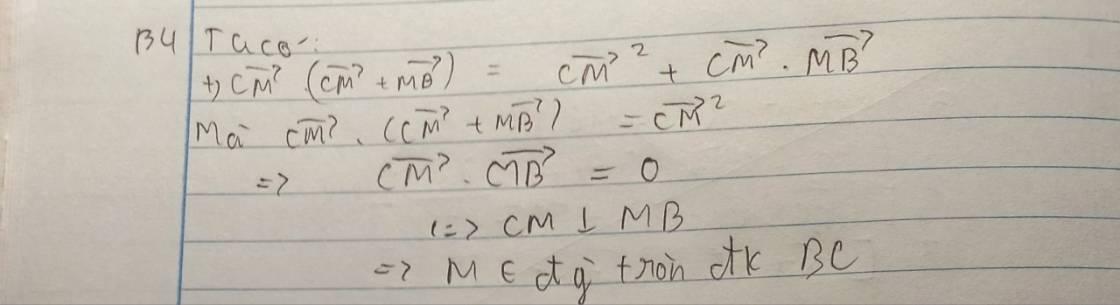

Gọi x là diện tích trồng đậu, y là diện tích trồng cà, (đơn vị a = 100 m2m2), điều kiện x≥0,y≥0x≥0,y≥0, ta có x+y≤8x+y≤8.
Số công cần dùng là 20x+30y≤18020x+30y≤180 hay 2x+3y≤182x+3y≤18.
Số tiền thu được là
F=3000000x+4000000yF=3000000x+4000000y(đồng)
Hay F=3x+4yF=3x+4y (triệu đồng)
Ta cần tìm x, y thỏa mãn hệ bất phương trình ⎧⎪ ⎨⎪ ⎩x+y≤82x+3y≤18x≥0y≥0{x+y≤82x+3y≤18x≥0y≥0
Sao cho F=3x+4yF=3x+4y đạt giá trị lớn nhất.
Biểu diễn tập nghiệm của (H) ta được miền tứ giác OABC với A(0;6), B(6;2), C(8;0) và O(0;0).
Xét giá trị của F tại các đỉnh O, A, B, C và so sánh ta suy ra x=6,y=2x=6,y=2 (tọa độ điểm B) là diện tích cần trồng mỗi loại để thu được nhiều tiền nhất là F = 26 (triệu đồng).
Đáp số: Trồng 6(a) đậu, 2(a) cà, thu hoạch 26 000 000 đồng.