Tìm số dư của phép chia
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Kẻ đường cao \(AH\)
Xét \(\Delta AHD\)vuông tại \(H\), có: \(\widehat{D}=30^o\)
\(\Rightarrow DH=\frac{AD}{2}=\frac{8}{2}=4\left(cm\right)\)(Áp dụng tính chất trong tam giác vuông , cạnh đối diện với góc 30 độ thì bằng 1 nửa cạnh huyền)
Áp dụng định lý Py-ta-go cho \(\Delta AHD\)vuông tại \(H\), ta có:
\(AH^2=AD^2-DH^2=8^2-4^2=64-16=48\)
\(\Rightarrow AH=\sqrt{48}=4\sqrt{3}\left(cm\right)\)
Ta có : \(S_{ABCD}=\frac{\left(AB+CD\right)AH}{2}=\frac{\left(7+9\right).4\sqrt{3}}{2}=32\sqrt{3}\left(cm^2\right)\)
Vậy \(S_{ABCD}=32\sqrt{3}cm^2\)

Sửa đề : \(B=\frac{x+3}{x+1}-\frac{2x-1}{1-x}+\frac{x+7}{x^2-1}\)
\(=\frac{x+3}{x+1}+\frac{2x-1}{x-1}+\frac{x+7}{x^2-1}\)
\(=\frac{\left(x+3\right)\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}+\frac{\left(2x-1\right)\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}+\frac{x+7}{\left(x+1\right)\left(x-1\right)}\)
\(=\frac{x^2-x+3x-3+2x^2+2x-x-1+x+7}{\left(x+1\right)\left(x-1\right)}\)
\(=\frac{x^2+4x+3}{\left(x+1\right)\left(x-1\right)}=\frac{\left(x+1\right)\left(x+3\right)}{\left(x+1\right)\left(x-1\right)}=\frac{x+3}{x-1}\)
\(B=\frac{x+3}{x+1}-\frac{2x-1}{1-x}+\frac{x+7}{x^2-1}\)
\(=\frac{x+3}{x+1}+\frac{2x-1}{x-1}+\frac{x+7}{\left(x+1\right)\left(x-1\right)}\)
\(=\frac{\left(x+3\right)\left(x-1\right)}{\left(x+1\right)\left(x-1\right)}+\frac{\left(2x-1\right)\left(x+1\right)}{\left(x+1\right)\left(x-1\right)}+\frac{x+7}{\left(x+1\right)\left(x-1\right)}\)
\(=\frac{x^2+2x-3}{\left(x+1\right)\left(x-1\right)}+\frac{2x^2+x-1}{\left(x+1\right)\left(x-1\right)}+\frac{x+7}{\left(x+1\right)\left(x-1\right)}\)
\(=\frac{x^2+2x-3+2x^2+x-1+x+7}{\left(x+1\right)\left(x-1\right)}\)
\(=\frac{3x^2+4x+3}{\left(x+1\right)\left(x-1\right)}\)

\(2+\frac{x}{5}-0,5x=1-\frac{2x}{4}+0,25\)
\(2+\frac{x}{5}-\frac{1}{2}x=1+0,25-\frac{x}{2}\)
\(2+\frac{x}{5}-\frac{x}{2}=1,25-\frac{x}{2}\)
\(\frac{x}{5}-\frac{x}{2}+\frac{x}{2}=-2+1,25\)
\(\frac{2x-5x+5x}{10}=0,75\)
\(\frac{2x}{5}=0,75\)
\(2x=0,75.5\)
\(2x=3,75\)
\(x=\frac{3,75}{2}=\frac{15}{8}\)
Vậy \(x=\frac{15}{8}\)

e) \(x^2-6x+9=45-5x^2\)
\(\Leftrightarrow6x^2-6x-36=0\)
\(\Leftrightarrow x^2-x-6=0\)
\(\Leftrightarrow\left(x+2\right)\left(x-3\right)=0\Rightarrow\orbr{\begin{cases}x=-2\\x=3\end{cases}}\)
f) \(\left(3x-2\right)^2=\left(x+5\right)^2\)
\(\Leftrightarrow\left(3x-2\right)^2-\left(x+5\right)^2=0\)
\(\Leftrightarrow\left(2x-7\right)\left(4x+3\right)=0\Leftrightarrow\orbr{\begin{cases}x=\frac{7}{2}\\x=-\frac{4}{3}\end{cases}}\)
g) \(\left(x^2-6x\right)^2+14\left(x-3\right)^2=81\)
\(\Leftrightarrow x^4-12x^3+36x^2+14\left(x^2-6x+9\right)=81\)
\(\Leftrightarrow x^4-12x^3+50x^2-84x+45=0\)
\(\Leftrightarrow\left(x^4-x^3\right)-\left(11x^3-11x^2\right)+\left(39x^2-39x\right)-\left(45x-45\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x^3-11x^2+39-45\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left[\left(x^3-3x^2\right)-\left(8x^2-24x\right)+\left(15x-45\right)\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-3\right)\left(x^2-8x+15\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left(x-3\right)^2\left(x-5\right)=0\)
\(\Rightarrow x\in\left\{1;3;5\right\}\)
h) \(\left(x^2-5x\right)^2+10\left(x^2-5x\right)+24=0\)
\(\Leftrightarrow\left(x^2-5x+5\right)^2=1\)
\(\Leftrightarrow\orbr{\begin{cases}x^2-5x+5=1\\x^2-5x+5=-1\end{cases}}\Leftrightarrow\orbr{\begin{cases}\left(x-1\right)\left(x-4\right)=0\\\left(x-2\right)\left(x-3\right)=0\end{cases}}\)
\(\Rightarrow x\in\left\{1;2;3;4\right\}\)
e, \(x^2-6x+9=45-5x^2\)
\(\Leftrightarrow\left(x-3\right)^2=5\left(9-x^2\right)\)
\(\Leftrightarrow\left(x-3\right)^2=5\left(3-x\right)\left(x+3\right)\)
\(\Leftrightarrow\left(x-3\right)+5\left(x-3\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left(x-3\right)\left[5+\left(x+3\right)\right]=0\)
\(\Leftrightarrow\left(x-3\right)\left(x+8\right)=0\Leftrightarrow x=3;-8\)
f, \(\left(3x-2\right)^2=\left(x+5\right)^2\)
\(\Leftrightarrow\left(3x-2\right)^2-\left(x+5\right)^2=0\)
\(\Leftrightarrow\left(3x-2-x-5\right)\left(3x-2+x+5\right)=0\)
\(\Leftrightarrow\left(2x-7\right)\left(4x+3\right)=0\Leftrightarrow x=\frac{7}{2};-\frac{3}{4}\)

\(x+y+z=7\Rightarrow z=7-x-y\Rightarrow xy+z-6=xy+7-x-y-6=xy-x-y+1\)
\(=\left(x-1\right)\left(y-1\right)\)
Tương tự: \(yz+x-6=\left(y-1\right)\left(z-1\right);zx+y-6=\left(z-1\right)\left(x-1\right)\)
Viết lại: \(H=\frac{1}{\left(x-1\right)\left(y-1\right)}+\frac{1}{\left(y-1\right)\left(z-1\right)}+\frac{1}{\left(z-1\right)\left(x-1\right)}\)
\(=\frac{x-1+y-1+z-1}{\left(x-1\right)\left(y-1\right)\left(z-1\right)}=\frac{x+y+z-3}{xyz-\left(xy+yz+zx\right)+x+y+z-1}\)
\(=\frac{7-3}{3-13+7-1}=-1\)(Từ gt tính được \(xy+yz+zx=13\))
Ta có :
\(xy+yz+zx\)= \(\frac{\left(x+y+z\right)^2-x^2-y^2-z^2}{2}\)= \(\frac{7^2-23}{2}\)= \(13\)
Ta lại có :
\(xy+z-6=xy+z+1-x-y-z\)= \(\left(x-1\right)\left(y-1\right)\)
\(\Rightarrow A=\)\(\frac{1}{\left(x-1\right)\left(y-1\right)}\)\(+\)\(\frac{1}{\left(y-1\right)\left(z-1\right)}\)\(+\)\(\frac{1}{\left(z-1\right)\left(x-1\right)}\)
\(=\)\(\frac{x+y+z-3}{xyz-xy-yz-zx+x+y+z-1}\)
\(=-1\)

a) Ta có: \(x^2+2y^2+2z^2-2xy-2yz-2z=4\)
\(\Leftrightarrow\left(x^2-2xy+y^2\right)+\left(y^2-2yz+z^2\right)+\left(z^2-2z+1\right)=5\)
\(\Leftrightarrow\left(x-y\right)^2+\left(y-z\right)^2+\left(z-1\right)^2=5\)
Mà \(5=0^2+1^2+2^2\) nên ta có dễ dàng xét được các TH
Làm tiếp nhé!
b) Ta có: \(x^2+13y^2-6xy=100\)
\(\Leftrightarrow\left(x^2-6xy+9y^2\right)+4y^2=100\)
\(\Leftrightarrow\left(x-3y\right)^2=100-4y^2\)
Mà \(\hept{\begin{cases}\left(x-3y\right)^2\ge0\\100-4y^2\le100\end{cases}}\Rightarrow0\le100-4y^2\le100\)
\(\Rightarrow y\in\left\{0;\pm1;\pm2;\pm3;\pm4;\pm5\right\}\)
Ta có các TH sau:
Nếu \(y=0\Rightarrow x^2=100\Rightarrow x=\pm10\)
Nếu \(y=\pm3\Leftrightarrow\orbr{\begin{cases}\left(x-9\right)^2=64\\\left(x+9\right)^2=64\end{cases}}\Rightarrow x\in\left\{17;1;-17;-1\right\}\)
... Tự làm tiếp nhé

Ta có: \(3x^2+10xy+8y^2=96\)
\(\Leftrightarrow\left(3x^2+6xy\right)+\left(4xy+8y^2\right)=96\)
\(\Leftrightarrow3x\left(x+2y\right)+4y\left(x+2y\right)=96\)
\(\Leftrightarrow\left(3x+4y\right)\left(x+2y\right)=96\) Từ đó ta giải PT nghiệm nguyên ra (Hơi nhiều TH đấy nhé)
Đến phần Ư(96) bạn chỉ cần sử dụng tính chẵn lẻ là sẽ loại bỏ bớt đi 1 số trường hợp rồi

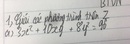
\(x^{41}\div x^2+1\)
Ta có:\(x^{41}=x^{41}-x+x=x\left(x^{40}-1\right)+x\)
Vì \(x^{40}-1=\left(x^4\right)^{10}-1^{10}⋮x^4-1\)
Mà \(x^4-1=\left(x^2-1\right)\left(x^2+1\right)⋮x^2+1\)
Nên \(x^{41}\)chia \(x^2-1\)dư \(x\)