Có 10 túi đựng tiền hình dạng giống hệt nhau. Trong đó, có 1 chiếc túi đựng tiền giả. Những đồng tiền giả nhẹ hơn 1 gam so với đồng tiền thật nặng 10 gam. Bằng 1 chiếc cân đồng hồ và chỉ 1 lần cân, hãy tìm ra túi đựng tiền giả?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
LD
Cho x,y,z là ba số lớn hơn 0 thỏa mãn: x+y+z=1.Chứng minh rằng:xy+yz+zx nhỏ hơn hoặc bằng 2/7+9xyz/7
0
CT
29 tháng 11 2021
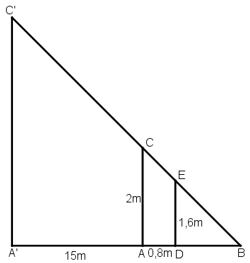
Gọi chiều cao của cây là h = A'C' và cọc tiêu AC = 2m.
Khoảng cách từ chân đến mắt người đo là DE = 1,6m.
Cọc xa cây một khoảng A'A = 15m, và người cách cọc một khoảng AD = 0,8m và gọi B là giao điểm của C'E và A'A.
Ta có: A’C’ ⊥ A’B, AC ⊥ A’B, DE ⊥ A’B
⇒ A’C’ // AC // DE.
Ta có: ΔDEB 
ΔACB (vì DE // AC)
Mà AB – DB = AD = 0,8
⇒ BD = 0,8.4 =3,2m; AB = 5.0,8 = 4m.
⇒ A'B = A'A + AD + DB = 15 + 0,8 + 3,2 = 19m
+ ΔACB ΔA’C’B (vì AC // A’C’)
Vậy cây cao 9,5m.
LV
0
28 tháng 11 2021
EM MỚI LỚP 3 LÊN EM KO BIẾT GÌ HẾT
CHẮC CHỊ HOẶC ANH NÊN TRA GOOGLE
LV
giúp mik nha mik đang cần gấp
0
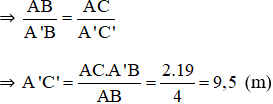
Đánh số các túi từ 1 đến 10
Túi thứ nhất lấy 1 đồng tiền
Túi thứ 2 lấy 2 đồng tiền
......................................
Túi thứ 10 lấy 10 đồng tiền
Tổng các đồng tiền lấy ra ở các túi là
\(1+2+3+...+10=\frac{10\left(1+10\right)}{2}=55\) đồng tiền
Nếu 55 đồng tiền đều là tiền thật thì chúng nặng là
55x10=550 gam
Cân 55 đồng tiền lấy ra xem chúng nhẹ hơn 550 gam là bao nhiêu gam thì đó chính là sô thứ tự của túi đựng tiền mà trong đó là tiền giả