Xét ΔABC vuông tại A có \(sinB=\dfrac{AC}{BC}\)

=>\(\dfrac{AC}{15}=\dfrac{3}{5}\)

=>\(AC=15\cdot\dfrac{3}{5}=9\left(cm\right)\)

ΔABC vuông tại A

=>\(AB^2+AC^2=BC^2\)

=>\(AB=\sqrt{15^2-9^2}=12\left(cm\right)\)

Tam giác `ABC` vuông tại `A`

`=> AC =  BC . sinB = 15 . 3/5 = 9 (cm)`

Và `AB =` \(\sqrt{BC^2-AC^2}=\sqrt{15^2-9^2}=\sqrt{144}=12\) `(cm)`

Bạn đang muốn hỏi về vấn đề gì ạ?

Điều kiện \(\overline{9,2x8}\)\(>\)\(92,78\) do đó \(x\)có 1 chữ số 

\(\Rightarrow x\)\(=\)\(8;9\)

Thay vào ta đc:\(9,288;9,298\)

Vậy \(x\)\(=\)\(8;9\)

x>10,35

mà x là số tự nhiên bé nhất

nên x=11

x= 11 

x<17,2<y

mà x,y là các số tự nhiên chẵn

nên (x,y)\(\in\left\{0;18\right\}\)

`17,2 > x `

`=> x` là `0;2;4;...;14` hoặc `16`

`17,2 < y`

`=> y` là `18;20;22`;.... (vô hạn) 

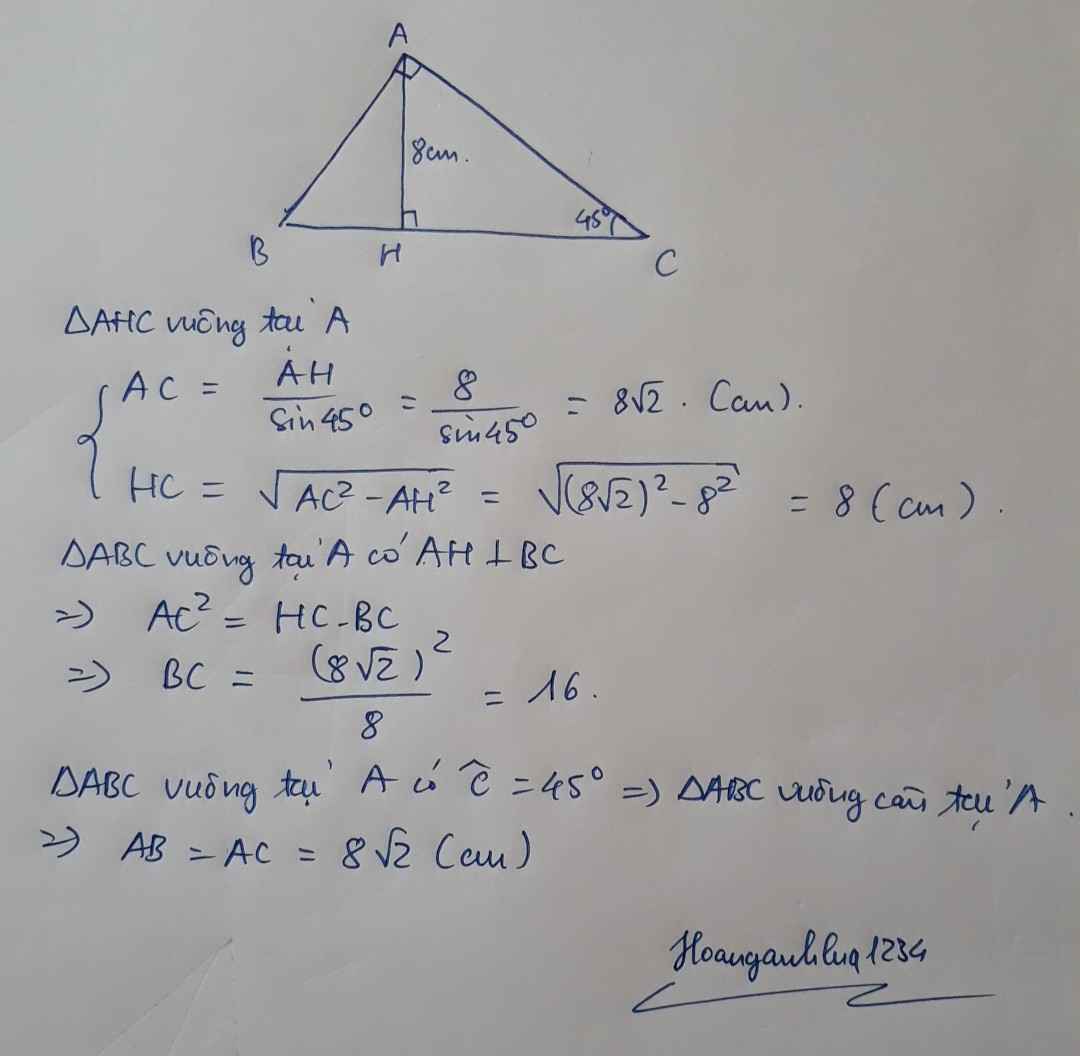
Xét ΔAHC vuông tại H có \(tanC=\dfrac{AH}{HC}\)

=>\(\dfrac{8}{HC}=tan45=1\)

=>HC=8(cm)

Xét ΔABC vuông tại A có AH là đường cao

nên \(AH^2=HB\cdot HC\)

=>\(HB\cdot8=8^2\)

=>HB=8(cm)

BC=BH+CH=8+8=16(cm)

ΔAHC vuông tại H

=>\(HA^2+HC^2=AC^2\)

=>\(AC=\sqrt{8^2+8^2}=8\sqrt{2}\left(cm\right)\)

ΔAHB vuông tại H

=>\(HA^2+HB^2=AB^2\)

=>\(AB=\sqrt{8^2+8^2}=8\sqrt{2}\left(cm\right)\)

Nửa chu vi sân trường là 142:2=71(m)

Chiều dài sân trường là (71+13):2=84:2=42(m)

Chiều rộng sân trường là 42-13=29(m)

Diện tích sân trường là:

42x29=1218(m²)