
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\dfrac{4}{\sqrt{5}+\sqrt{3}}-\sqrt{20}\\ =\dfrac{4\left(\sqrt{5}-\sqrt{3}\right)}{\left(\sqrt{5}+\sqrt{3}\right)\left(\sqrt{5}-\sqrt{3}\right)}-\sqrt{20}\\ =\dfrac{4\left(\sqrt{5}-\sqrt{3}\right)}{\left(\sqrt{5}\right)^2-\left(\sqrt{3}\right)^2}-\sqrt{2^2\cdot5}\\ =\dfrac{4\left(\sqrt{5}-\sqrt{3}\right)}{5-3}-2\sqrt{5}\\ =\dfrac{4\left(\sqrt{5}-\sqrt{3}\right)}{2}-2\sqrt{5}\\ =2\left(\sqrt{5}-\sqrt{3}\right)-2\sqrt{5}\\ =2\sqrt{5}-2\sqrt{3}-2\sqrt{5}\\ =-2\sqrt{3}\)

Xét \(f\left(x\right)=VT=x^2+y^2+xy-3x-3y+3\)
\(=x^2+\left(y-3\right)x+y^2-3y+3\)
Có \(\Delta=\left(y-3\right)^2-4\left(y^2-3y+3\right)\)
\(=y^2-6y+9-4y^2+12y-12\)
\(=-3y^2+6y-3\)
\(=-3\left(y-1\right)^2\le0\) với mọi \(y\inℝ\)
Mà \(f\left(x\right)\) có hệ số cao nhất bằng \(1>0\) nên từ đây có \(VT=f\left(x\right)\ge0\)
Dấu "=" xảy ra khi \(y=1\). Khi đó \(\Delta=0\) nên pt \(f\left(x\right)=0\) có nghiệm kép \(\Leftrightarrow\) \(x=\dfrac{-\left(y-3\right)}{2}=1\).
Ta có đpcm.
Cho $x, \, y$ là hai số thực lớn hơn $\sqrt{2}$. Chứng minh rằng $x^4-x^3y+x^2y^2-xy^3+y^4>x^2+y^2$.


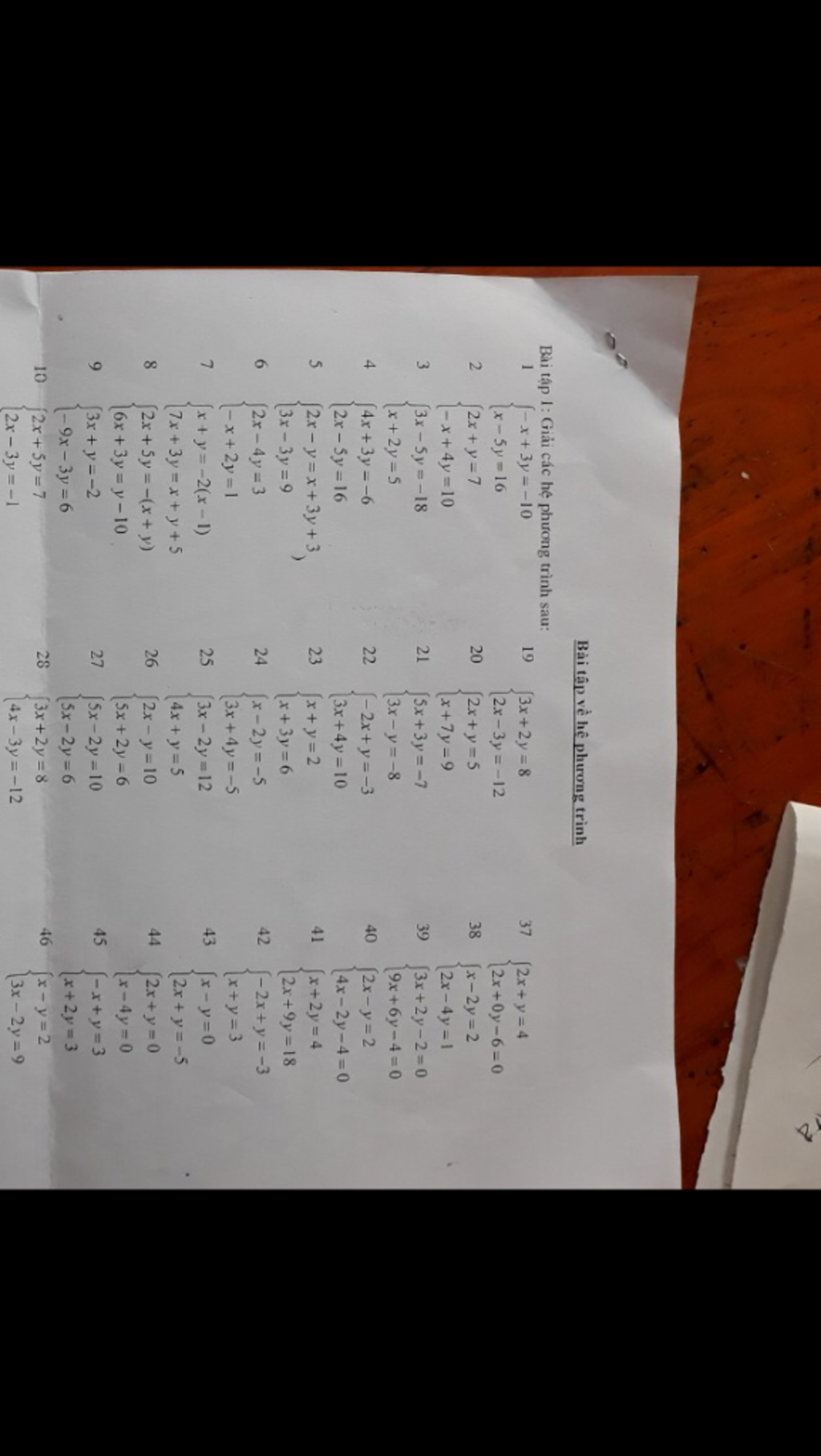
\(1.\left\{{}\begin{matrix}-x+3y=-10\\x-5y=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2y=6\\x-5y=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{6}{-2}=-3\\x-5\cdot\left(-3\right)=16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-3\\x+15=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-3\\x=16-15=1\end{matrix}\right.\\ 2.\left\{{}\begin{matrix}2x+y=7\\-x+4y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+y=7\\-2x+8y=20\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+y=7\\9x=27\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}2x+y=7\\x=\dfrac{27}{9}=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2\cdot3+y=7\\x=3\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=7-6=1\\x=3\end{matrix}\right.\)
\(3.\left\{{}\begin{matrix}3x-5y=-18\\x+2y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-5y=-18\\3x+6y=15\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-3\\x+2\cdot\left(-3\right)=5\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=-3\\x=5+6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-3\\x=11\end{matrix}\right.\\ 4.\left\{{}\begin{matrix}4x+3y=-6\\2x-5y=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x+3y=-6\\4x-10y=32\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}13y=-38\\2x-5y=16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-38}{13}\\2x-5\cdot\dfrac{-38}{13}=16\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-38}{13}\\2x+\dfrac{190}{13}=16\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-38}{13}\\2x=16-\dfrac{190}{13}=\dfrac{18}{13}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-38}{13}\\x=\dfrac{18}{13}:2=\dfrac{9}{13}\end{matrix}\right.\)
20: \(\left\{{}\begin{matrix}2x+y=5\\x+7y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+y=5\\2x+14y=18\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+14y-2x-y=18-5\\2x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}13y=13\\2x=5-y\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=1\\2x=5-1=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\x=2\end{matrix}\right.\)
21: \(\left\{{}\begin{matrix}5x+3y=-7\\3x-y=-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x+3y=-7\\9x-3y=-24\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5x+3y+9x-3y=-7-24\\3x-y=-8\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}14x=-31\\y=3x+8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=-\dfrac{31}{14}\\y=3\cdot\dfrac{-31}{14}+8=-\dfrac{93}{14}+\dfrac{112}{14}=\dfrac{19}{14}\end{matrix}\right.\)
22: \(\left\{{}\begin{matrix}-2x+y=-3\\3x+4y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-3+2x\\3x+4\left(2x-3\right)=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=2x-3\\3x+8x-12=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11x=22\\y=2x-3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\y=2\cdot2-3=4-3=1\end{matrix}\right.\)
23: \(\left\{{}\begin{matrix}x+y=2\\x+3y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x+3y-x-y=6-2\\x+y=2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2y=4\\x+y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=2-y=2-2=0\end{matrix}\right.\)
24: \(\left\{{}\begin{matrix}x-2y=-5\\3x+4y=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-4y=-10\\3x+4y=-5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-4y+3x+4y=-10-5\\x-2y=-5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}5x=-15\\2y=x+5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\2y=-3+5=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-3\\y=1\end{matrix}\right.\)
25: \(\left\{{}\begin{matrix}3x-2y=12\\4x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-2y=12\\8x+2y=10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x-2y+8x+2y=12+10\\4x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}11x=22\\y=5-4x\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=2\\y=5-4\cdot2=5-8=-3\end{matrix}\right.\)
26: \(\left\{{}\begin{matrix}2x-y=10\\5x+2y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x-2y=20\\5x+2y=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4x-2y+5x+2y=20+6\\2x-y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x=26\\y=2x-10\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{26}{9}\\y=2x-10=2\cdot\dfrac{26}{9}-10=\dfrac{52}{9}-10=-\dfrac{38}{9}\end{matrix}\right.\)
27: \(\left\{{}\begin{matrix}5x-2y=10\\5x-2y=6\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x-2y-5x+2y=10-6\\5x-2y=6\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}0x=4\\2y=5x-6\end{matrix}\right.\Leftrightarrow\left(x;y\right)\in\varnothing\)
28: \(\left\{{}\begin{matrix}3x+2y=8\\4x-3y=-12\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}12x+8y=32\\12x-9y=-36\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}12x+8y-12x+9y=32+36\\3x+2y=8\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}17y=68\\3x=8-2y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=4\\3x=8-2\cdot4=8-8=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=0\\y=4\end{matrix}\right.\)
37: \(\left\{{}\begin{matrix}2x+y=4\\2x+0y-6=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x=6\\y=4-2x=4-6=-2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=3\\y=-2\end{matrix}\right.\)
38: \(\left\{{}\begin{matrix}x-2y=2\\2x-4y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-4y=4\\2x-4y=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-4y-2x+4y=4-1\\x-2y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}0y=3\\x-2y=2\end{matrix}\right.\)
=>\(\left(x;y\right)\in\varnothing\)
39: \(\left\{{}\begin{matrix}3x+2y-2=0\\9x+6y-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+2y=2\\9x+6y=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}9x+6y=6\\9x+6y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}0y=2\\3x+2y=2\end{matrix}\right.\Leftrightarrow\left(x;y\right)\in\varnothing\)
40: \(\left\{{}\begin{matrix}2x-y=2\\4x-2y-4=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x-y=2\\4x-2y=4\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x-y=2\\2x-y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}0x=0\\y=2x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\in R\\y=2x-2\end{matrix}\right.\)
41: \(\left\{{}\begin{matrix}x+2y=4\\2x+9y=18\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}2x+4y=8\\2x+9y=18\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}2x+9y-2x-4y=18-8\\x+2y=4\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5y=10\\x=4-2y\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=2\\x=4-2\cdot2=4-4=0\end{matrix}\right.\)
42: \(\left\{{}\begin{matrix}-2x+y=-3\\x+y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-2x+y-x-y=-3-3\\x+y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-3x=-6\\y=3-x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=3-2=1\end{matrix}\right.\)
43: \(\left\{{}\begin{matrix}x-y=0\\2x+y=-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-y+2x+y=0-5\\x=y\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x=-5\\y=x\end{matrix}\right.\Leftrightarrow y=x=-\dfrac{5}{3}\)
44: \(\left\{{}\begin{matrix}2x+y=0\\x-4y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-2x\\x-4\cdot\left(-2x\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}9x=0\\y=-2x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=-2\cdot0=0\end{matrix}\right.\)
45: \(\left\{{}\begin{matrix}-x+y=3\\x+2y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-x+y+x+2y=3+3\\x+2y=3\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3y=6\\x=3-2y\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=3-2\cdot2=3-4=-1\end{matrix}\right.\)
46: \(\left\{{}\begin{matrix}x-y=2\\3x-2y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-3y=6\\3x-2y=9\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}3x-3y-2x+2y=6-9\\x-y=2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-y=-3\\x=y+2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=3\\x=3+2=5\end{matrix}\right.\)

\(\dfrac{3}{4}x-6< =0\)
=>\(\dfrac{3}{4}x< =6\)
=>\(x< =6:\dfrac{3}{4}=6\cdot\dfrac{4}{3}=8\)

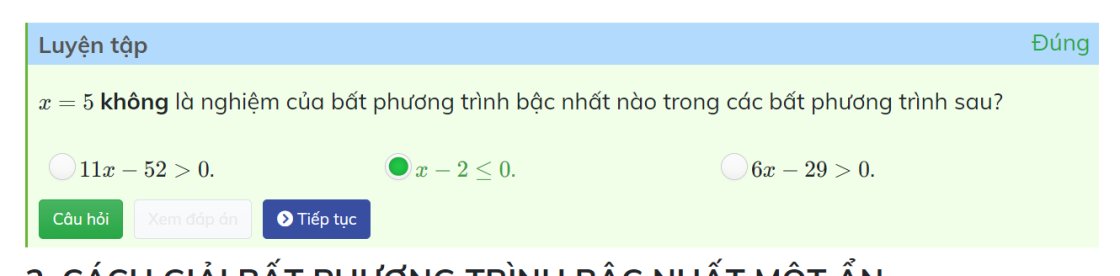
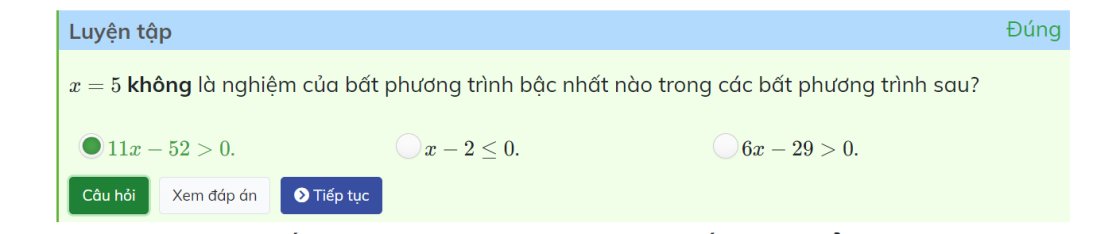
Khi x=5 thì \(11x-52=11\cdot5-52=55-52=3>0\)
=>Đúng
Khi x=5 thì \(6x-29=6\cdot5-29=30-29=1>0\)
=>6x-29>0 đúng
Khi x=5 thì 5-2=3<=0(sai)
=>x-2<=0 là đáp án sai duy nhất, hai cái còn lại đúng
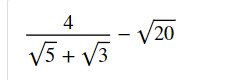

a: Xét tứ giác ABOC có \(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)
nên ABOC là tứ giác nội tiếp
b: Xét (O) có
\(\widehat{ABE}\) là góc tạo bởi tiếp tuyến BA và dây cung BE
\(\widehat{BFE}\) là góc nội tiếp chắn cung BE
Do đó: \(\widehat{ABE}=\widehat{BFE}\)
Xét ΔABE và ΔAFB có
\(\widehat{ABE}=\widehat{AFB}\)
\(\widehat{BAE}\) chung
Do đó: ΔABE~ΔAFB
=>\(\dfrac{AB}{AF}=\dfrac{AE}{AB}\)
=>\(AB^2=AF\cdot AE\)
c: Xét (O) có
AB,AC là các tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1),(2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại X
ΔOEF cân tại O
mà OD là đường trung tuyến
nên OD\(\perp\)FE tại D
Xét ΔAXK vuông tại X và ΔADO vuông tại D có
\(\widehat{XAK}\) chung
Do đó: ΔAXK~ΔADO
=>\(\dfrac{AX}{AD}=\dfrac{AK}{AO}\)
=>\(AX\cdot AO=AD\cdot AK\)
Xét ΔABO vuông tại B có BX là đường cao
nên \(AX\cdot AO=AB^2\)
=>\(AE\cdot AF=AK\cdot AD\)
Ta có: \(\widehat{ADO}=\widehat{ABO}=\widehat{ACO}=90^0\)
=>A,D,B,C,O cùng thuộc đường tròn đường kính AO