\(M=\frac{\sqrt{x}}{\sqrt{x}+1}\left(x\ge0\right)\)

Khi \(M=\sqrt{x}-2\)

\(\Rightarrow\frac{\sqrt{x}}{\sqrt{x}+1}=\sqrt{x}-2\)

\(\Leftrightarrow\sqrt{x}=\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)\)

\(\Leftrightarrow\sqrt{x}=x+\sqrt{x}-2\sqrt{x}-2\)

\(\Leftrightarrow\sqrt{x}=x-\sqrt{x}-2\)

\(\Leftrightarrow x-\sqrt{x}-\sqrt{x}-2=0\)

\(\Leftrightarrow x-2\sqrt{x}+1-3=0\)

\(\Leftrightarrow\left(\sqrt{x}-1\right)^2=3\)

\(\Leftrightarrow\left(\sqrt{x}-1\right)^2=\left(\pm\sqrt{3}\right)^2\)

\(\Leftrightarrow\sqrt{x}-1=\pm\sqrt{3}\)

\(\Leftrightarrow\sqrt{x}=\pm\sqrt{3}+1\)

\(\Leftrightarrow\orbr{\begin{cases}x=\left(\sqrt{3}+1\right)^2\\x=\left(-\sqrt{3}+1\right)^2\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x=3+2\sqrt{3}+1\\1-2\sqrt{3}+3\end{cases}}\)

\(\Leftrightarrow\orbr{\begin{cases}x=4+2\sqrt{3}\\x=4-2\sqrt{3}\end{cases}}\)

Vậy \(x\in\left\{4\pm2\sqrt{3}\right\}\)khi \(M=\sqrt{x}-2\)

bài dễ quá ; làm ny mik đi ; mik giải cho :v 

(x+2)(x+3)(x+8)(x+12)=4x2

Ta nhóm như sau: [(x+2)(x+12)][(x+3)(x+8)]=4x2

<=> (x2 + 14x + 24)(x2 + 11x +24) = 4x2

Vì x = 0 , không phải nghiệm của pt nên chia cả hai vế của pt cho x2 \(\ne\) 0, ta có:

\(\left(x+14+\frac{24}{x}\right)\left(x+11+\frac{24}{x}\right)=4\)

 0, ta có:

Đặt: \(x+\frac{24}{x}=y\)ta có: (y+14)(y+11)-4=4

<=> y2 + 24y+150 = 0

Giải pt ta được y1 = -10 ; y2 = -15 ⇒\(\orbr{\begin{cases}x^2+10x+24=0\\x^2+15x+24=0\end{cases}}\)

Pt có 4 nghiệm x1 = -4 ; x2 = -6 ; x3,4 = \(\frac{-15\pm\sqrt{129}}{2}\)

bạn cho mình hỏi là tại sao mình bị mất phần bạn bè và phần tin nhắn tren OLM vậy hả các bạn ?

mình cũng không biết nữa 

ai giúp mình với ạ

Ta thấy x=0 không là nghiệm của phương trình

chia cả 2 vế cho x^2 ta được:

PT <=> x^2-3x-6+3/x+1/(x^2)=0

       <=> (x^2-2+1/(x^2))-3(x-1/x)-4=0

      <=> (x-1/x)^2-3(x-1/x)-4=0

Đặt x-1/x=y

PT <=> y^2-3y-4=0

     <=> y=-4 hoặc y=1

^HT^

Vì x=0 không là nghiệm của pt.Chia cả hai vế của pt với x2≠0x2≠0 ta đc:

x2−3x+6+3x+1x2=0x2−3x+6+3x+1x2=0

⇔(x2+1x2)−3(x−1x)+6=0⇔(x2+1x2)−3(x−1x)+6=0

Đặt x−1x=t⇒x2+1x2−2=t2⇒x2+1x2=t2+2x−1x=t⇒x2+1x2−2=t2⇒x2+1x2=t2+2

khi đó pt trở thành:

t2+2−3t+6=0t2+2−3t+6=0

⇔t2−3t+8=0⇔t2−3t+8=0

=> pt vô nghiệm

x4−3x3−2x2+6x+4=0x4−3x3−2x2+6x+4=0

⇔x4−2x3−2x2−x3+2x2+2x−2x2+4x+4=0⇔x4−2x3−2x2−x3+2x2+2x−2x2+4x+4=0

⇔x2(x2−2x−2)−x(x2−2x−2)−2(x2−2x−2)=0⇔x2(x2−2x−2)−x(x2−2x−2)−2(x2−2x−2)=0

⇔(x2−x−2)(x2−2x−2)=0⇔(x2−x−2)(x2−2x−2)=0

⇔(x+1)(x−2)(x−1−√3)(x−1+√3)=0⇔(x+1)(x−2)(x−1−3)(x−1+3)=0

⇔⎡⎢ ⎢ ⎢ ⎢⎣x=−1x=2x=1+√3x=1−√3

tl

x4−3x3−2x2+6x+4=0x4−3x3−2x2+6x+4=0

⇔x4−2x3−2x2−x3+2x2+2x−2x2+4x+4=0⇔x4−2x3−2x2−x3+2x2+2x−2x2+4x+4=0

⇔x2(x2−2x−2)−x(x2−2x−2)−2(x2−2x−2)=0⇔x2(x2−2x−2)−x(x2−2x−2)−2(x2−2x−2)=0

⇔(x2−x−2)(x2−2x−2)=0⇔(x2−x−2)(x2−2x−2)=0

⇔(x+1)(x−2)(x−1−√3)(x−1+√3)=0⇔(x+1)(x−2)(x−1−3)(x−1+3)=0

⇔⎡⎢ ⎢ ⎢ ⎢⎣x=−1x=2x=1+√3x=1−√3

^HT^

trả lời :

bài bé quá bn òi

mk ko nhìn thấy

Bài bé quá, bn đăng lại câu hỏi đi

Câu b bạn ạ.

TL

Em đoán là 4!!
HT

trả lời :
mk cũng đoán là 4 ko bt nhưng nghĩ thì cx 

hợp lý

^HT^

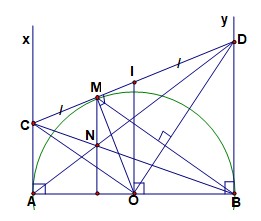
Bài 3: 

1. Vì CM,CA là tiếp tuyến của (O)

\(\rightarrow OC\)  là phân giác \(\widehat{AOM},CM=CA\)

Tương tự \(OD\) là phân giác \(\widehat{BOM},DM=DB\)

\(\rightarrow AC+BD=CM+DM=DB\)

2. Từ câu 1:

\(\rightarrow\widehat{COD}=\widehat{COM}+\widehat{MOD}=\frac{1}{2}\widehat{AOM}+\frac{1}{2}\widehat{MOB}=90^o\)

3. Ta có:

\(OC\perp OD,OM\perp CD\rightarrow CM.DM=OM^2\)

Mà  \(AC=CM,DM=DB,OM=R\rightarrow AC.BD=R^2=\frac{AB^2}{4}\)

4. Vì  \(CA,CM\) là tiếp tuyến của (O)

\(\rightarrow OC\perp AM\)

Mà \(AM\perp BM\) vì AB là đường kính của (O)

\(\rightarrow OC//BM\)

5. Lấy I là trung điểm CD vì \(\widehat{COD}=90^o\rightarrow\left(I,IO\right)\)  là đường tròn đường kính CD

Mà O là trung điểm AB, \(AC//DB\left(\perp AB\right)\) 

\(\rightarrow IO\) là đường trung bình hình thang  \(\text{◊}ABCD\)

\(\rightarrow IO//AC\rightarrow IO\perp AB\)

\(\rightarrow AB\) là tiếp tuyến của (I,IO)

Hay AB là tiếp tuyến của đường tròn đường kính CD

6. Ta có : \(AC//BD,CM,CA,DM,DA\)

\(\rightarrow\frac{NA}{ND}=\frac{AC}{BD}=\frac{CM}{MD}\)

\(MN//AC\rightarrow MN\perp AB\left(AC\perp AB\right)\)

7. Để \(ABCD\) có chu vi nhỏ nhất

\(\rightarrow AB+BD+AC+CD\) nhỏ nhất

\(\rightarrow AB+CD+CD\) nhỏ nhất

\(\rightarrow AB+2CD\) nhỏ nhất

\(\rightarrow CD\) nhỏ nhất

Mà \(CD\ge AB\) vì  \(ABCD\)  là hình thang vuông tại A,B

Dấu = xảy ra khi \(CD//AB\rightarrow M\) nằm giữa A và B