cho đường tròn (O;R) đường kính AB. Lấy điểm M thuộc (O) sao cho góc MAB=60 và điểm C thuộc đường kính AB, kẻ CH song song với BM. Tia phân giác của góc MAB cắt đường tròn tại E và cắt CH tại F, dường thẳng MF cắt đường tròn tại N. a/ chứng minh tứ giác AFCN nội tiếp đường tròn. b/ Chứng minh góc MAF= góc FNC. Suy ra 3 điểm N, C, E thẳng hàng. C/ Tính theo r diện tích hình viên phân tạo bởi dây AE cung nhỏ AE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

2: \(P=\left(\dfrac{\sqrt{x}+1}{x-\sqrt{x}}+\dfrac{\sqrt{x}-2}{x-1}\right):\dfrac{1}{x-1}\)
\(=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}-1\right)}+\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\cdot\dfrac{x-1}{1}\)
\(=\dfrac{\left(\sqrt{x}+1\right)^2+\sqrt{x}\left(\sqrt{x}-2\right)}{\sqrt{x}\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{x-1}{1}\)
\(=\dfrac{x+2\sqrt{x}+1+x-2\sqrt{x}}{\sqrt{x}}=\dfrac{2x+1}{\sqrt{x}}\)


\(C=\dfrac{1}{\sqrt{x}+2}+\dfrac{1}{\sqrt{x}-2}+\dfrac{4}{x-4};\left(x\ge0;x\ne4\right)\)
\(=\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{\sqrt{x}+2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}+\dfrac{4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}-2+\sqrt{x}+2+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{2\sqrt{x}+4}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{2\left(\sqrt{x}+2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}=\dfrac{2}{\sqrt{x}-2}\)

\(x^2-\left(2m+1\right)x+m^2+1=0\)
\(\text{Δ}=\left(2m+1\right)^2-4\cdot1\cdot\left(m^2+1\right)\)
\(=4m^2+4m+1-4m^2-4=4m-3\)
Để phương trình có hai nghiệm phân biệt thì Δ>0
=>4m-3>0
=>4m>3
=>\(m>\dfrac{3}{4}\)
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2m+1\\x_1x_2=\dfrac{c}{a}=m^2+1\end{matrix}\right.\)
\(A=\left(2x_1-x_2\right)\left(x_1-2x_2\right)\)
\(=2x_1^2+2x_2^2-5x_1x_2\)
\(=2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]-5x_1x_2\)
\(=2\left[\left(2m+1\right)^2-2\left(m^2+1\right)\right]-5\left(m^2+1\right)\)
\(=2\left(2m+1\right)^2-9\left(m^2+1\right)\)
\(=2\left(4m^2+4m+1\right)-9m^2-9\)
\(=8m^2+8m+2-9m^2-9\)
\(=-m^2+8m-7\)
\(=-\left(m^2-8m+7\right)\)
\(=-\left(m^2-8m+16-9\right)\)
\(=-\left(m-4\right)^2+9< =9\forall m\)
Dấu '=' xảy ra khi m=4

ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x\ne9\end{matrix}\right.\)
\(\left|P\right|+P=0\)
=>|P|=-P
=>P<=0
=>\(\dfrac{3\sqrt{x}}{\sqrt{x}-3}< =0\)
=>\(\dfrac{\sqrt{x}}{\sqrt{x}-3}< =0\)
=>\(0< =\sqrt{x}< 3\)
=>\(0< =x< 9\)

Để hệ có nghiệm duy nhất thì \(\dfrac{1}{m}\ne\dfrac{m}{1}\)
=>\(m^2\ne1\)
=>\(m\notin\left\{1;-1\right\}\)
Sửa đề: \(\left\{{}\begin{matrix}x+my=m+1\\mx+y=2m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}mx+m^2y=m^2+m\\mx+y=2m\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y\left(m^2-1\right)=m^2-m\\x+my=m+1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}y=\dfrac{m\left(m-1\right)}{\left(m-1\right)\left(m+1\right)}=\dfrac{m}{m+1}\\x=m+1-my=m+1-\dfrac{m^2}{m+1}=\dfrac{2m+1}{m+1}\end{matrix}\right.\)
\(\left\{{}\begin{matrix}x>=2\\y>=1\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\dfrac{2m+1-2m-2}{m+1}>=0\\\dfrac{m-m-1}{m+1}>=0\end{matrix}\right.\)
=>\(-\dfrac{1}{m+1}>=0\)
=>m+1<0
=>m<-1
mà \(m\in\left(-10;10\right)\)
nên \(m\in\left\{-9;-8;...;-2\right\}\)
=>Có 8 số nguyên m thỏa mãn

a: Xét tứ giác MAOB có \(\widehat{MAO}+\widehat{MBO}=90^0+90^0=180^0\)
nên MAOB là tứ giác nội tiếp
b: Ta có; ΔOCD cân tại O
mà OK là đường trung tuyến
nên OK\(\perp\)CD tại K
Ta có: \(\widehat{OKM}=\widehat{OAM}=\widehat{OBM}=90^0\)
=>O,K,A,M,B cùng thuộc đường tròn đường kính OM
c: Xét (O) có
MA,MB là các tiếp tuyến
Do đó: MA=MB
=>M nằm trên đường trung trực của BA(1)
Ta có: OA=OB
=>O nằm trên đường trung trực của BA(2)
Từ (1),(2) suy ra OM là đường trung trực của AB
=>OM\(\perp\)AB tại H
Xét ΔOHN vuông tại H và ΔOKM vuông tại K có
\(\widehat{HON}\) chung
Do đó: ΔOHN~ΔOKM
=>\(\dfrac{OH}{OK}=\dfrac{ON}{OM}\)
=>\(OH\cdot OM=OK\cdot ON\left(3\right)\)
Xét ΔOAM vuông tại A có AH là đường cao
nên \(OH\cdot OM=OA^2=R^2\left(4\right)\)
Từ (3),(4) suy ra \(OK\cdot ON=R^2=OD^2\)
=>\(\dfrac{OK}{OD}=\dfrac{OD}{ON}\)
Xét ΔOKD và ΔODN có
\(\dfrac{OK}{OD}=\dfrac{OD}{ON}\)
\(\widehat{KOD}\) chung
Do đó: ΔOKD~ΔODN
=>\(\widehat{OKD}=\widehat{ODN}=90^0\)
=>ND là tiếp tuyến của (O)
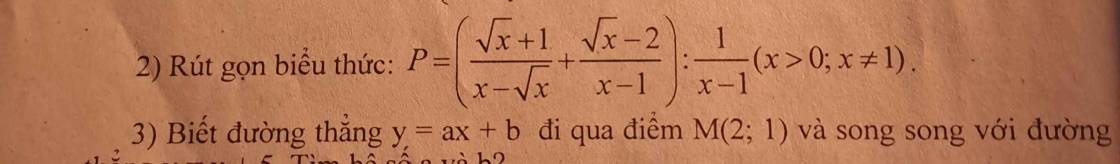
 cho a,b,c là độ dài 3 cạnh tam giác có chu vi bằng 4
cho a,b,c là độ dài 3 cạnh tam giác có chu vi bằng 4