Bài 39 (trang 123 SGK Toán 9 Tập 1)
Cho hai đường tròn $(O)$ và $(O')$ tiếp xúc ngoài tại $A$, Kẻ tiếp tuyến chung ngoài $BC$, $B \in (O)$, $C \in (O')$. Tiếp tuyến chung trong tại $A$ cắt tiếp tuyến chung ngoài $BC$ ở $I$.
a) Chứng minh rằng $\widehat{BAC} = 90^{\circ}$.
b) Tính số đo góc $OIO'$.
c) Tính độ dài $BC$, biết $OA = 9$cm, $O'A = 4$cm.

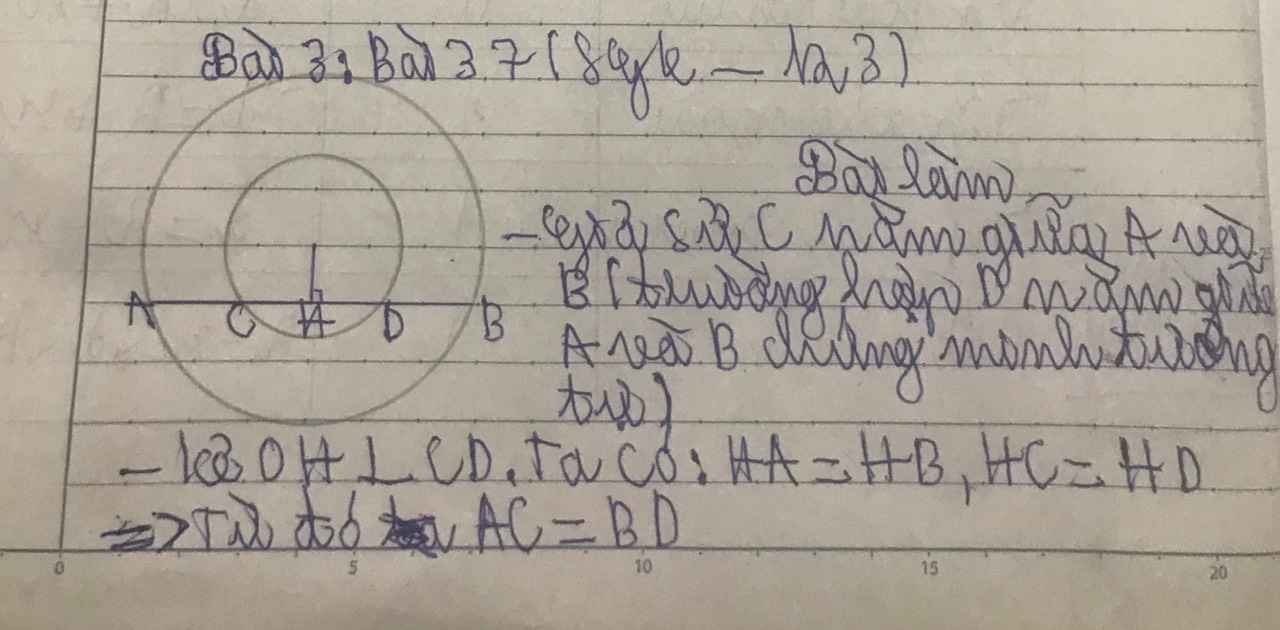





) Theo tính chất hai tiếp tuyến cắt nhau ta được IA = IB, IA = IC.
b) Theo tính chất hai tiếp tuyến cắt nhau ta có IO, IO' là các tia phân giác của hai góc kề bù AIB, AIC nên:
c) ΔOIO' vuông tại A có IA là đường cao nên theo hệ thức giữa cạnh và đường cao ta có:
IA2 = AO.AO' = 9.4 = 36
=> IA = 6 (cm)
Vậy BC = 2.IA = 2.6 = 12 (cm)
A B C O' O I 4 9
Bài làm
a) Ta thấy: BC là tiếp tuyến chung ngoài và tiếp tuyến chung trong của hai đường tròn (O') và (O) cắt nhau tại I
=> CI = IA = IB (theo tính chất hai tiếp tuyến cắt nhau)
Xét tam giác ABC có: IA = 1/2BC
=> Tam giác ABC vuông tại A
Do đó: góc BAC = 90o (đpcm)
b) Ta thấy: O'I là tia phân giác của CO'O (theo tính chất hai tiếp tuyến cắt nhau)
=> \(\widehat{IO'O}=\frac{1}{2}\widehat{CO'O}\Rightarrow2\widehat{IO'O}=\widehat{CO'O}\)
Ta lại thấy: OI là tia phân giác của BOO' (theo tính chất hai tiếp tuyến cắt nhau)
=> \(\widehat{IOO'}=\frac{1}{2}\widehat{BOO'}\Rightarrow2\widehat{IOO'}=\widehat{BOO'}\)
Xét tứ giác O'CBO có:
\(\widehat{O'CB}+\widehat{CBO}+\widehat{B\text{OO}'}+\widehat{\text{OO}'C}=360^0\)(tổng 4 góc của tứ giác)
Hay \(90^0+90^0+2\widehat{IO'O}+2\widehat{IOO'}=360^0\)
=> \(2\left(\widehat{IO'O}+\widehat{IOO'}\right)=360^0-90^0-90^0=180^0\)
=> \(\widehat{IO'O}+\widehat{IOO'}=\frac{180^0}{2}=90^0\)\
Xét tam giác O'IO có:
\(\widehat{IO'O}+\widehat{IOO'}+\widehat{O'IO}=180^0\)(Tổng ba góc trong tam giác)
Hay \(90^0+\widehat{\text{OIO}'}=180^0\)
=> \(\widehat{\text{OIO}'}=180^0-90^0=90^0\)
Vậy góc OIO' = 90o
c) Xét tam giác O'IO vuông tại I có:
Đường cao IA
Theo hệ thức lượng trong tam giác:
Ta có: IA2 = OA * O'A
hay IA2 = 4 * 9
=> IA = 6 (cm)
Mà IA = IC = IB = 6 (cm)
=> IC + IB = BC
hay BC = 6 + 6 = 12 (cm)
Vậy BC = 12cm