Chị Tâm là công nhân ở một khu công nghiệp , tiền lương mỗi tháng chị nhận là 7.000.000 đồng . Sau khi dùng 4/5 số tiền lương để trang trải chi phí sinh hoạt , chị dành 1 nửa số tiền còn lại để gửi tiết kiệm . Hỏi mỗi tháng chị Hà tiết kiệm được bao nhiêu tiền ?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




\(\dfrac{1}{1\text{x}2}+\dfrac{1}{2\text{x}3}+...+\dfrac{1}{2021\text{x}2022}\\ =\dfrac{1}{1}-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{2021}-\dfrac{1}{2022}\\ =\dfrac{1}{1}-\dfrac{1}{2022}\\ =\dfrac{2021}{2022}\)

a: Xét (O) có
ΔADB nội tiếp
AB là đường kính
Do đó: ΔADB vuông tại D
=>AD\(\perp\)DB tại D
Xét (O) có
SA,SD là các tiếp tuyến
Do đó: SA=SD
=>S nằm trên đường trung trực của AD(1)
ta có: OA=OD
=>O nằm trên đường trung trực của AD(2)
Từ (1),(2) suy ra SOlà đường trung trực của AD
=>SO\(\perp\)AD
Ta có: SO\(\perp\)AD
AD\(\perp\)DB
Do đó: SO//DB
b: Ta có: ΔADB vuông tại D
=>ΔADC vuông tại D
Ta có: \(\widehat{SAD}+\widehat{SCD}=90^0\)(ΔACD vuông tại D)
\(\widehat{SDA}+\widehat{SDC}=\widehat{ADC}=90^0\)
mà \(\widehat{SAD}=\widehat{SDA}\)(ΔSAD cân tại S)
nên \(\widehat{SCD}=\widehat{SDC}\)
=>SC=SD
=>SC=SA(3)
c: Ta có: DH\(\perp\)AB
CA\(\perp\)AB
Do đó: DH//CA
Xét ΔBCS có DE//CS
nên \(\dfrac{DE}{SC}=\dfrac{BE}{BS}\left(4\right)\)
Xét ΔBAS có EH//SA
nên \(\dfrac{EH}{SA}=\dfrac{BE}{BS}\left(5\right)\)
Từ (3),(4),(5) suy ra DE=EH
=>E là trung điểm của DH

c: \(\dfrac{5\cdot4^6\cdot9^4-3^9\cdot\left(-8\right)^4}{4\cdot2^{13}\cdot3^8+2\cdot8^4\cdot\left(-27\right)^3}\)
\(=\dfrac{5\cdot2^{12}\cdot3^8-3^9\cdot2^{12}}{2^{15}\cdot3^8-2^{13}\cdot3^9}\)
\(=\dfrac{2^{12}\cdot3^8\left(5-3\right)}{2^{13}\cdot3^8\left(2^2-3\right)}=\dfrac{2^{13}}{2^{13}}=1\)

Vì 27=3x3x3, suy ra cạnh của hình lập phương là 3dm.
S1 mặt của hình lập phương là:
3×3=9(dm²)
Đs 9dm².
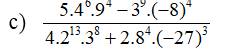

số tiền còn lại là :
7.000.000 * 4/5 = 5 . 600.000(đồng)
mỗi tháng chị gửi tiết kiệm được là:
5.600.000: 2= 2.800.000 (đồng)
ghi chú :* là nhân
Sai rùi! Bạn hãy đọc kĩ lại đi
Bởi vì chị đã dành một nửa số tiện tiết kiệm còn lại để gửi tiết kiệm cơ mà!