Tìm nghiệm của các đa thức a) f(x)=2x+5 b)-5x-1/2 c) h(x)=6x-12 d) h(x)=ax+b (với a,b là các hằng số)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có \(\dfrac{7-x}{13+y}=\dfrac{7}{13}\Rightarrow\dfrac{7-x}{7}=\dfrac{13+y}{13}\)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\dfrac{7-x}{7}=\dfrac{13+y}{13}=\dfrac{13+y-7+x}{13-7}=\dfrac{6+x+y}{6}=\dfrac{2022+6}{6}=338\)
\(\Rightarrow\left\{{}\begin{matrix}7-x=338\times7=2366\\13+y=338\times13=4394\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}x=-2359\\y=4381\end{matrix}\right.\)
Thầy,cô cho e hỏi tý là :" tại sao lại lấy 338 x 7 ạ ?"



a, \(A=\left(\dfrac{8}{3}xy^2\right).\left(\dfrac{-1}{4}x^2y^5\right).\left(10x^5y^7\right)^0\)
⇒\(A=\dfrac{8}{3}xy^2.\dfrac{-1}{4}x^2y^5.1\)
⇒\(A=\left(\dfrac{8}{3}.\dfrac{-1}{4}.1\right).\left(x.x^2\right).\left(y^2.y^5\right)\)
⇒\(A=\dfrac{-2}{3}x^3y^7\)
+)Hệ số: \(\dfrac{-2}{3}\)
+)Bậc:10
b, Thay \(x=2\), \(y=-1\) vào A ta có:
\(A=\dfrac{-2}{3}.2^3.\left(-1\right)^7\)
⇒\(A=\dfrac{-2}{3}.8.\left(-1\right)\)
⇒\(A=\dfrac{16}{3}\)
Vậy \(A=\dfrac{16}{3}\) khi \(x=2,y=-1\)
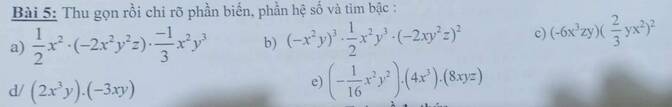
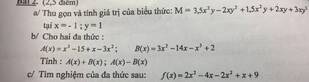
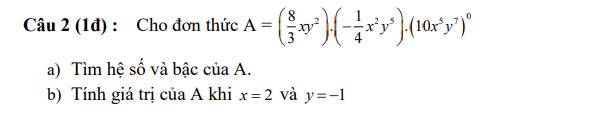 giúp mình với, mình cảm ơn nhiều
giúp mình với, mình cảm ơn nhiều