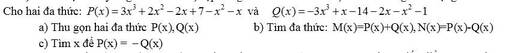
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\left(2x-3\right)\left(\dfrac{5}{2}-x\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}2x-3=0\\\dfrac{5}{2}-x=0\end{matrix}\right.\)\(\Rightarrow\left[{}\begin{matrix}2x=3\\x=\dfrac{5}{2}-0\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=\dfrac{5}{2}\end{matrix}\right.\)
\(x-12=\dfrac{1}{2}\)
\(\Rightarrow x=\dfrac{1}{2}+12\Rightarrow x=\dfrac{25}{2}\)
\(\left(2x+\dfrac{3}{5}\right)^2-\dfrac{9}{25}=0\)
\(\Rightarrow\left(2x+\dfrac{3}{5}\right)^2=\left(\pm\dfrac{3}{5}\right)^2\Rightarrow\left[{}\begin{matrix}2x+\dfrac{3}{5}=\dfrac{3}{5}\\2x+\dfrac{3}{5}=-\dfrac{3}{5}\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{3}{5}\end{matrix}\right.\)
\(\dfrac{7}{3}x-\dfrac{5}{2}x=-\dfrac{1}{3}\)
\(\Rightarrow\left(\dfrac{7}{3}-\dfrac{5}{2}\right)x=-\dfrac{1}{3}\Rightarrow-\dfrac{1}{6}x=-\dfrac{1}{3}\Rightarrow x=2\)
\(\dfrac{3}{4}+\dfrac{1}{4}:x=1\)
\(\Rightarrow\dfrac{1}{4}:x=\dfrac{1}{4}\Rightarrow x=1\)
\(\dfrac{1}{3}+\dfrac{2}{5}.\left(x+1\right)=1\)
\(\Rightarrow\dfrac{1}{3}+\dfrac{2}{5}x+\dfrac{2}{5}=1\Rightarrow\dfrac{2}{5}x=\dfrac{4}{15}\Rightarrow x=\dfrac{2}{3}\)

\(=\left(2x^5-2x^5\right)+\left(3x^2+x^2\right)+\left(-x^4+x^4\right)+\left(3x-x\right)+\left(-3-2\right)\\ =4x^2+2x-5\)


tgian học ở trường = 1/3.24 = 8 (h) tgian học ở nhà = 1/8.24 = 3(h) tgian học ở trường = 1/6.24 = 4(h) tgian trông em = 1/3.3 = 1(h) tgian rảnh = 24-8-3-4-1 = 8 (h)

\(2\left(x+y\right)=5\left(y+z\right)=3\left(z+x\right)\Leftrightarrow\dfrac{x+y}{15}=\dfrac{y+z}{6}=\dfrac{z+x}{10}\)
Đặt \(\dfrac{x+y}{15}=\dfrac{y+z}{6}=\dfrac{z+x}{10}=t\).
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(t=\dfrac{x+y}{15}=\dfrac{y+z}{6}=\dfrac{z+x}{10}=\dfrac{x+y+y+z+z+x}{15+6+10}=\dfrac{2\left(x+y+z\right)}{31}\)
Suy ra \(x+y=15t,y+z=6t,z+x=10t,x+y+z=\dfrac{31}{2}t\)
\(\Rightarrow\left\{{}\begin{matrix}x=\dfrac{19}{2}t\\y=\dfrac{11}{2}t\\z=\dfrac{1}{2}t\end{matrix}\right.\)
