Tìm x biết: 3x + 7 = 3 - x
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án:
Giải thích các bước giải:
a) F(x) = 3x – 6
F(x) = 0 ⇔ 3x – 6 = 0
⇔ 3x = 6
⇔ x = 2
b) U(y) = -5y + 30
U(y) = 0 ⇔ -5y + 30 = 0
⇔ -5y = -30
⇔ y = 6
c) G(z) = (z – 3) (16 – 4z)
G(z) = 0 ⇔
)
⇔
a) Để cho đa thức F(x) có nghiệm thì \(3x-6=0\)
\(\Rightarrow3x=6\)
\(\Rightarrow x=6:3\)
\(\Rightarrow x=2\)
b) Để cho đa thức U(y) có nghiệm thì \(-5y+30=0\)
\(\Rightarrow-5y=30\)
\(\Rightarrow y=30:-5\)
\(\Rightarrow y=6\)
c) Để cho đa thức G(z) có nghiệm thì \(\left(z-3\right)\left(16-4z\right)=4\left(z-3\right)\left(4-z\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}z-3=0\\4-z=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}z=3\\z=4\end{matrix}\right.\)

a/
Hai tg ABD và tg BCD có chung đường cao từ B->AC nên
\(\dfrac{S_{ABD}}{S_{BCD}}=\dfrac{AD}{CD}=\dfrac{1}{2}\)
Hai tg ABD và tg BCD có chung BD nên
\(\dfrac{S_{ABD}}{S_{BCD}}=\) đường cao từ A->BD / đường cao từ C->BD = \(\dfrac{1}{2}\)
Hai tg ABI và tg BCI có chung BI nên
\(\dfrac{S_{ABI}}{S_{BCI}}=\)đường cao từ A->BD / đường cao từ C->BD = \(\dfrac{1}{2}\)
\(\Rightarrow S_{ABI}=\dfrac{1}{2}S_{BCI}\) (1)
Hai tg BMI và tg BCI có chung đường cao từ I->BC nên
\(\dfrac{S_{BMI}}{S_{BCI}}=\dfrac{BM}{BC}=\dfrac{1}{2}\Rightarrow S_{BMI}=\dfrac{1}{2}S_{BCI}\) (2)
Từ (1) và (2) \(\Rightarrow S_{ABI}=S_{BMI}\) Hai tg này có chung đường cao từ B->AM nên
\(\dfrac{S_{ABI}}{S_{BMI}}=\dfrac{AI}{MI}=1\Rightarrow AI=MI\)
b/
Hai tg ABI và tg BMI có chung đường cao từ B->AM và AI=MI
\(\Rightarrow S_{ABI}=S_{BMI}\) (1)
Hai tg BMI và tg BCI có chung đường cao từ I->BC nên
\(\dfrac{S_{BMI}}{S_{BCI}}=\dfrac{BM}{BC}=\dfrac{1}{2}\) (2)
Từ (1) và (2) \(\Rightarrow\dfrac{S_{ABI}}{S_{BCI}}=\dfrac{1}{2}\)
Hai tg ABI và tg BCI có chung BI nên
\(\dfrac{S_{ABI}}{S_{BCI}}=\) đường cao từ A->BD / đường cao từ C->BD =\(\dfrac{1}{2}\)
Hai tg AID và tg CID có chung ID nên
\(\dfrac{S_{AID}}{S_{CID}}=\)đường cao từ A->BD / đường cao từ C->BD =\(\dfrac{1}{2}\)
Hai tg AID và tg CID chung đường cao từ I->AC nên
\(\dfrac{S_{AID}}{S_{CID}}=\dfrac{AD}{CD}=\dfrac{1}{2}\Rightarrow AD=\dfrac{1}{2}CD\)

Lời giải:
$P(0)=a.0+b=b=2007$
$P(1)=a.1+b=a+b=2006$
$\Rightarrow a=2006-b=2006-2007=-1$
Vậy $a=-1; b=2007$

a) \(\dfrac{1}{2}-\left(x+\dfrac{1}{3}\right)=\dfrac{5}{6}\)
\(\Rightarrow x+\dfrac{1}{3}=\dfrac{1}{2}-\dfrac{5}{6}\)
\(\Rightarrow x+\dfrac{1}{3}=\dfrac{3}{6}-\dfrac{5}{6}\)
\(\Rightarrow x+\dfrac{1}{3}=-\dfrac{2}{6}\)
\(\Rightarrow x=-\dfrac{2}{6}-\dfrac{1}{3}\)
\(\Rightarrow x=-\dfrac{2}{3}\)
b) \(\left(\dfrac{3}{8}-\dfrac{1}{5}\right)+\left(\dfrac{5}{8}-x\right)=\dfrac{1}{5}\)
\(\Rightarrow\left(\dfrac{15}{40}-\dfrac{8}{40}\right)+\left(\dfrac{5}{8}-x\right)=\dfrac{1}{5}\)
\(\Rightarrow\dfrac{7}{40}+\left(\dfrac{5}{8}-x\right)=\dfrac{1}{5}\)
\(\Rightarrow\dfrac{5}{8}-x=\dfrac{1}{5}-\dfrac{7}{40}\)
\(\Rightarrow\dfrac{5}{8}-x=\dfrac{1}{40}\)
\(\Rightarrow x=\dfrac{5}{8}-\dfrac{1}{40}\)
\(\Rightarrow x=\dfrac{3}{5}\)

a) x=7-\dfrac{2}{5}+1,62=8,22x=7−52+1,62=8,22
b) x=4 \dfrac{3}{5}+\dfrac{1}{5}-\dfrac{1}{2}=4 \dfrac{3}{10}x=453+51−21=4103
c) 2 x-x=\dfrac{3}{5}+\dfrac{4}{7}2x−x=53+74
x=\dfrac{41}{35}x=3541
d) x=3 \dfrac{1}{2}-\dfrac{5}{7}+\dfrac{1}{13}-0.25x=321−75+131−0.25
x=2 \dfrac{223}{364}x=2364223
x=7-\dfrac{2}{5}+1,62=8,22x=7−52+1,62=8,22
b) x=4 \dfrac{3}{5}+\dfrac{1}{5}-\dfrac{1}{2}=4 \dfrac{3}{10}x=453+51−21=4103
c) 2 x-x=\dfrac{3}{5}+\dfrac{4}{7}2x−x=53+74
x=\dfrac{41}{35}x=3541
d) x=3 \dfrac{1}{2}-\dfrac{5}{7}+\dfrac{1}{13}-0.25x=321−75+131−0.25
x=2 \dfrac{223}{364}x=2364223

\(a)\left(\dfrac{1}{2}+1,5\right)x=\dfrac{1}{5}\)
\(\Rightarrow2x=\dfrac{1}{5}\)
\(\Rightarrow x=\dfrac{1}{10}\)
\(b)\left(-1\dfrac{3}{5}+x\right):\dfrac{12}{13}=2\dfrac{1}{6}\)
\(\Leftrightarrow-\dfrac{8}{5}+x=\dfrac{13}{6}.\dfrac{12}{13}\)
\(\Leftrightarrow-\dfrac{8}{5}+x=2\)
\(\Leftrightarrow x=\dfrac{18}{5}\)
\(c)\left(x:2\dfrac{1}{3}\right).\dfrac{1}{7}=-\dfrac{3}{8}\)
\(\Leftrightarrow x:\dfrac{7}{3}=-\dfrac{3}{8}:\dfrac{1}{7}\)
\(\Leftrightarrow x=-\dfrac{21}{8}.\dfrac{7}{3}\)
\(\Leftrightarrow x=-\dfrac{49}{8}\)
\(d)-\dfrac{4}{7}x+\dfrac{7}{5}=\dfrac{1}{8}:\left(-1\dfrac{2}{3}\right)\)
\(\Leftrightarrow-\dfrac{4}{7}x+\dfrac{7}{5}=-\dfrac{3}{40}\)
\(\Leftrightarrow-\dfrac{4}{7}x=-\dfrac{59}{40}\)
\(\Leftrightarrow x=\dfrac{413}{160}\)
a)\left(\dfrac{1}{2}+1,5\right) \cdot x=\dfrac{1}{5}(21+1,5)⋅x=51
2 \cdot x=\dfrac{1}{5}2⋅x=51
x=\dfrac{1}{5}: 2x=51:2
x=\dfrac{1}{10} x=101
b) \left(-1 \dfrac{3}{5}+x\right): \dfrac{12}{13}=2 \dfrac{1}{6}(−153+x):1312=261
-1 \dfrac{3}{5}+x=\dfrac{13}{6} \cdot \dfrac{12}{13}−153+x=613⋅1312
x=2+1 \dfrac{3}{5}x=2+153
x=3 \dfrac{3}{5} x=353
c) \left(x: 2 \dfrac{1}{3}\right) \cdot \dfrac{1}{7}=\dfrac{-3}{8}(x:231)⋅71=8−3
x \cdot \dfrac{3}{7} \cdot \dfrac{1}{7}=\dfrac{-3}{8}x⋅73⋅71=8−3
x=\dfrac{-3}{8}: \dfrac{3}{49}x=8−3:493
x=\dfrac{-49}{8}=-6 \dfrac{1}{8}x=8−49=−681
d) \dfrac{-4}{7} \cdot x+\dfrac{7}{5}=\dfrac{1}{8}:\left(-1 \dfrac{2}{3}\right)7−4⋅x+57=81:(−132)
\dfrac{-4}{7} x+\dfrac{7}{5}=\dfrac{1}{8} \cdot \dfrac{-3}{5}7−4x+57=81⋅5−3
-\dfrac{4}{7} x=\dfrac{-3}{40}-\dfrac{7}{5} \\ x=\dfrac{-59}{40}: \dfrac{-4}{7}=\dfrac{413}{160}=2 \dfrac{93}{160}−74x=40−3−57x=40−59:7−4=160413=216093
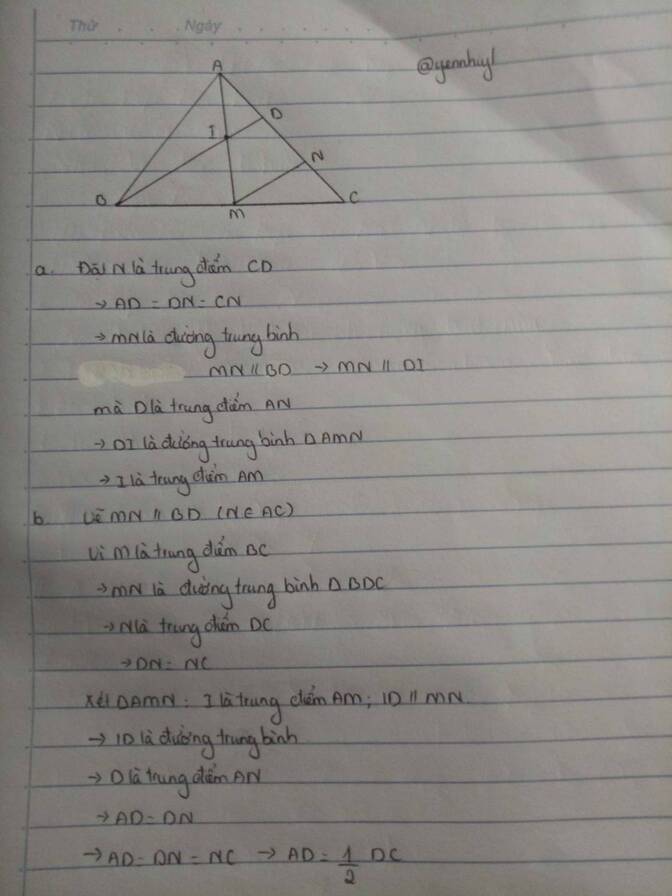


3x + 7 = 3 - x
<=> 3x + x = 3 - 7
<=> 4x = -4
<=> x = -4/4
<=> x= -1
Vâỵ S{ -1}