Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
a. $A(x)=(-5x^4+5x^4)+(3x^3-x^3)-2x-3=2x^3-2x-3$
b.
Thay $x=1$ vào đa thức $A(x)$ thì:
$A(1)=2.1^3-2.1-3=-3\neq 0$ nên $x=1$ không phải nghiệm của đa thức $A(x)$

- hai góc xAt và góc tAy là hai góc kề bù
- hai góc xAz và góc zAy là hai góc kề bù


Vẽ hình ra nhé.
a. phythagores: AB = 6 , (100 2 - 8 2)
b
Hai tam giác vuông, có canh huyền chung nên bằng nhau
c.
BI là phân giác của tam giác cân ABD nhé, thì nó là đường trung trực.
d. tam giác BCE có hai đường cao có sẵn thì đường qua đỉnh và điểm cao chung cũng chính là đường cao thứ 3.
...........
1. Những dạng bài này trả lời tốn giờ, không có tích điểm cao, 4 câu chỉ được 1 GP, thì không vào nữa !
2.
OOLOLMOLM ccocócó ccucưcửacửa ssosôsổsổ rttrtratra llolơlờlờilời nnhnhunhưnhư vvavâvầvầyvầy dđđađâđâyđây!
OLM có của sổ trả lời cả đống lỗi !!!


Bạn cần giúp bài nào thì ghi chú rõ bài đó ra để mọi người nắm được. Đăng 1 cái đề dài ngoằng không ghi chú như thế này tỉ lệ giúp đỡ sẽ rất thấp.

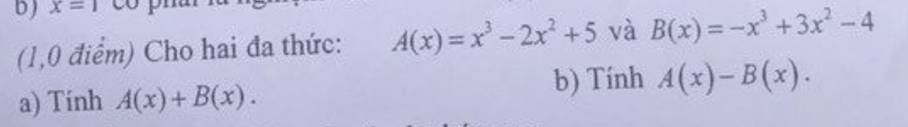 giúp mình với, gấp lắm ạ :<
giúp mình với, gấp lắm ạ :<
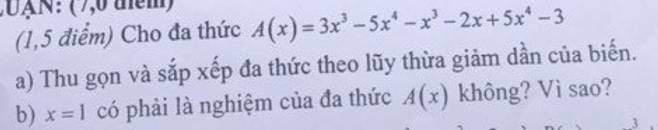 giúp mình vớii
giúp mình vớii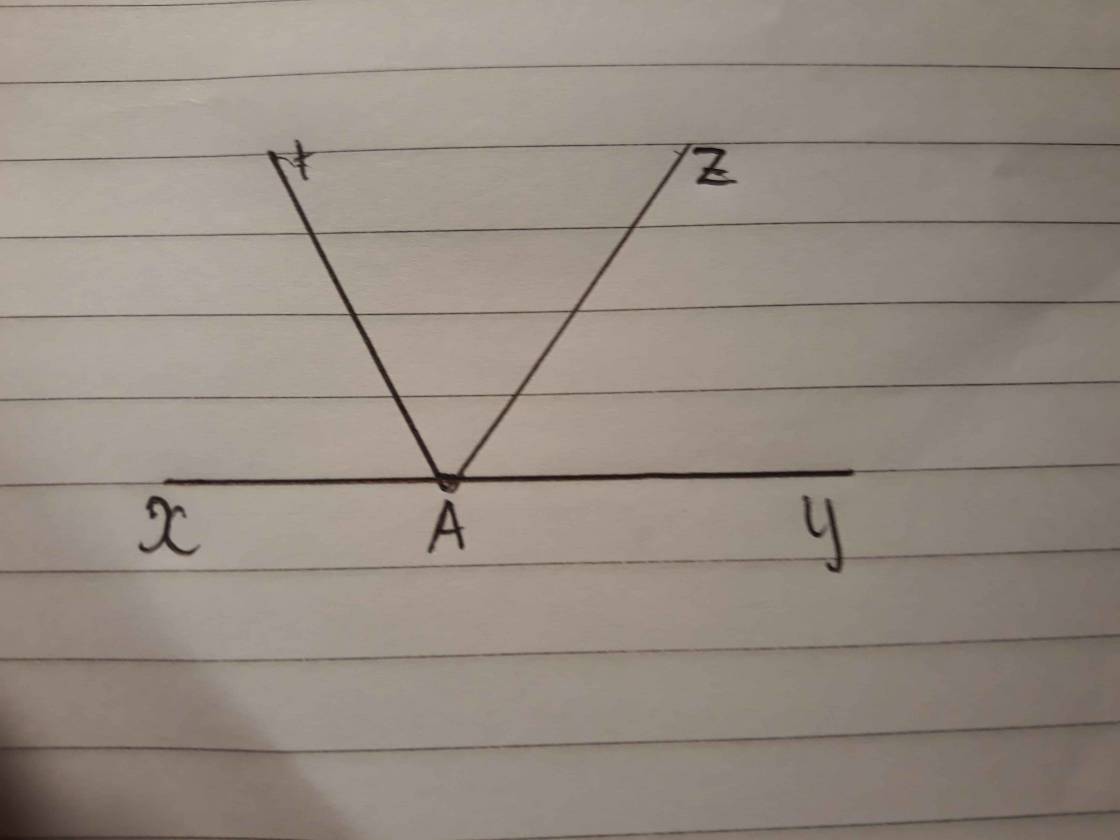
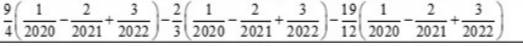



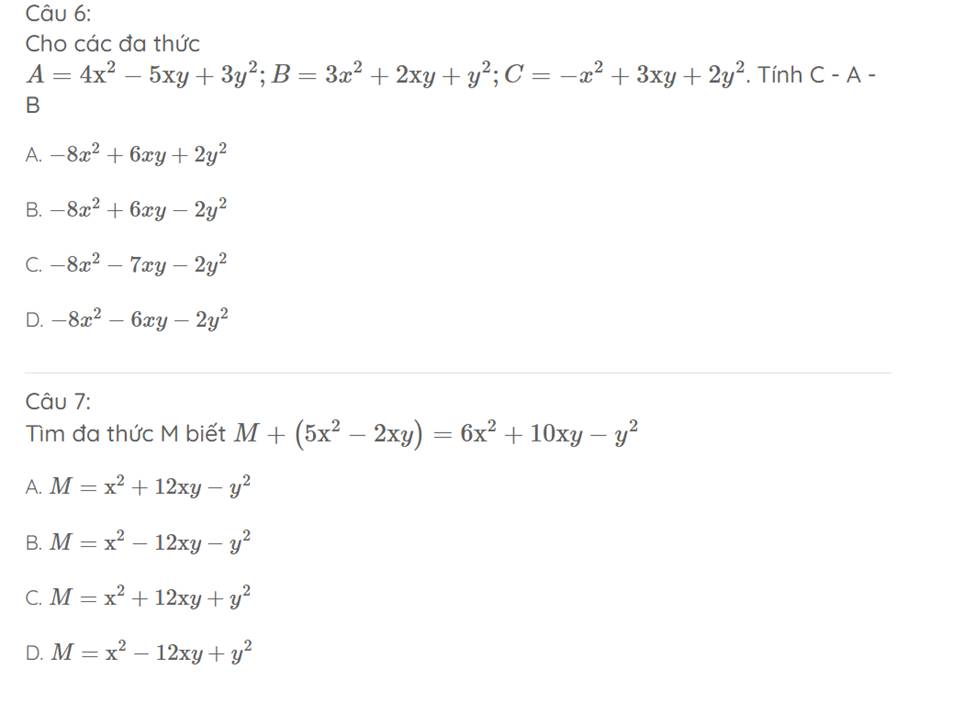
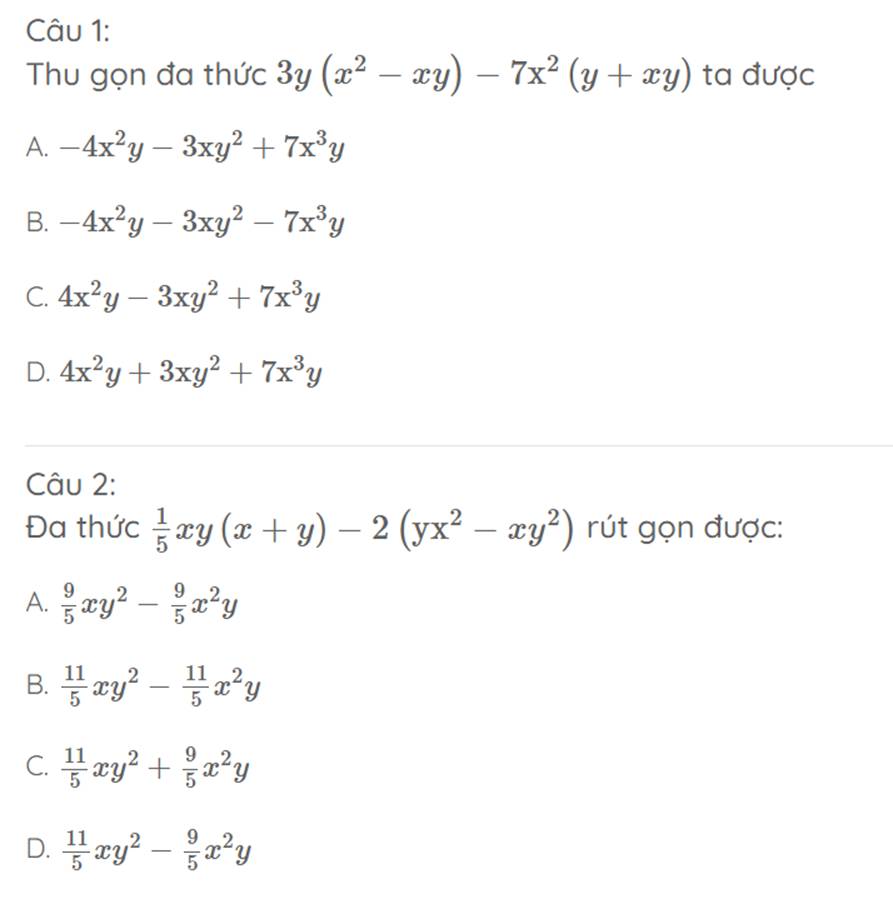


góc ACx và góc ACB là hai góc kề bù