a: Xét ΔABD vuông tại A và ΔHBD vuông tại H có

BD chung

\(\widehat{ABD}=\widehat{HBD}\)

Do đó: ΔBAD=ΔBHD

b: Xét ΔCAB vuông tại A và ΔCAE vuông tại A có

CA chung

AB=AE

Do đó: ΔCAB=ΔCAE

=>\(\widehat{ACB}=\widehat{ACE}\)

=>CA là phân giác của góc ECB

45,8-x+8,25=12,4:4

=>54,05-x=3,1

=>x=54,05-3,1=50,95

45,8 - x + 8,25 = 12,4 :4
45,8 - x + 8,25 = 3,1
45,8 - x            = 3,1 - 8,25
45,8 - x            = -5,15
          x            = 45,8 - (-5,15)
          x            = 50,95 
Vậy x = 50,95 

\(\dfrac{4}{5\times7}+\dfrac{4}{7\times9}+\dfrac{4}{9\times11}+\dfrac{4}{11\times13}+\dfrac{4}{13\times15}\) (sửa đề)

\(=2\times\left(\dfrac{2}{5\times7}+\dfrac{2}{7\times9}+\dfrac{2}{9\times11}+\dfrac{2}{11\times13}+\dfrac{2}{13\times15}\right)\)

\(=2\times\left(\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{15}\right)\)

\(=2\times\left(\dfrac{1}{5}-\dfrac{1}{15}\right)\)

\(=2\times\dfrac{2}{15}=\dfrac{4}{15}\)

Sửa đề: \(\dfrac{4}{5\times7}+\dfrac{4}{7\times9}+\dfrac{4}{9\times11}+\dfrac{4}{11\times13}+\dfrac{4}{13\times15}\)

Gọi A = \(\dfrac{4}{5\times7}+\dfrac{4}{7\times9}+\dfrac{4}{9\times11}+\dfrac{4}{11\times13}+\dfrac{4}{13\times15}\)

\(A=\dfrac{4}{5\times7}+\dfrac{4}{7\times9}+\dfrac{4}{9\times11}+\dfrac{4}{11\times13}+\dfrac{4}{13\times15}\\ A=2\times\left(\dfrac{2}{5\times7}+\dfrac{2}{7\times9}+\dfrac{2}{9\times11}+\dfrac{2}{11\times13}+\dfrac{2}{13\times15}\right)\\ A=2\times\left(\dfrac{1}{3}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+\dfrac{1}{9}-\dfrac{1}{11}+\dfrac{1}{11}-\dfrac{1}{13}+\dfrac{1}{13}-\dfrac{1}{15}\right)\\ A=2\times\left(\dfrac{1}{3}-\dfrac{1}{15}\right)\\ A=2\times\dfrac{4}{15}\\ A=\dfrac{8}{15}\)

Vậy \(A=\dfrac{8}{15}\)

\(\left(2x+2\right)^2=64\)

\(\Rightarrow\left(2x+2\right)^2=\left(\pm8\right)^2\)

\(\Rightarrow\left[{}\begin{matrix}2x+2=8\\2x+2=-8\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}2x=6\\2x=-10\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=3\\x=-5\end{matrix}\right.\)

Mà x là số tự nhiên nên \(x=3\).

Vậy \(x=3\).

Ta có

(2.x+2)²=64=8²=(-8)²

=> 2.x+2 = 8 =(-8)

\(\left[{}\begin{matrix}2.x+2=8\\2.x+2=-8\end{matrix}\right.\) => \(\left[{}\begin{matrix}2x=6\\2x=-10\end{matrix}\right.\) => \(\left[{}\begin{matrix}x=3\\x=-5\end{matrix}\right.\)

mà x là số tự nhiên nên x =3

Vậy x=3

\(B=\left(\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}-2}{x-1}\right)\cdot\dfrac{x\sqrt{x}+x-\sqrt{x}-1}{\sqrt{x}}\)

\(=\left(\dfrac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}-\dfrac{\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right)\cdot\dfrac{\left(\sqrt{x}+1\right)\left(x-1\right)}{\sqrt{x}}\)

\(=\dfrac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2\cdot\left(\sqrt{x}-1\right)}\cdot\dfrac{\left(\sqrt{x}+1\right)^2\cdot\left(\sqrt{x}-1\right)}{\sqrt{x}}\)

\(=\dfrac{x+\sqrt{x}-2-\left(x-\sqrt{x}-2\right)}{\sqrt{x}}=\dfrac{2\sqrt{x}}{\sqrt{x}}=2\)

=>B là số nguyên

a: Thay x=1 và y=1 vào (d), ta được:

\(a\cdot1+3=1\)

=>a+3=1

=>a=-2

b: a=-2 nên y=-2x+3

Thay x=-2 vào y=-2x+3, ta được:

\(y=-2\cdot\left(-2\right)+3=7=y_B\)

Vậy: B(-2;7) thuộc (d)

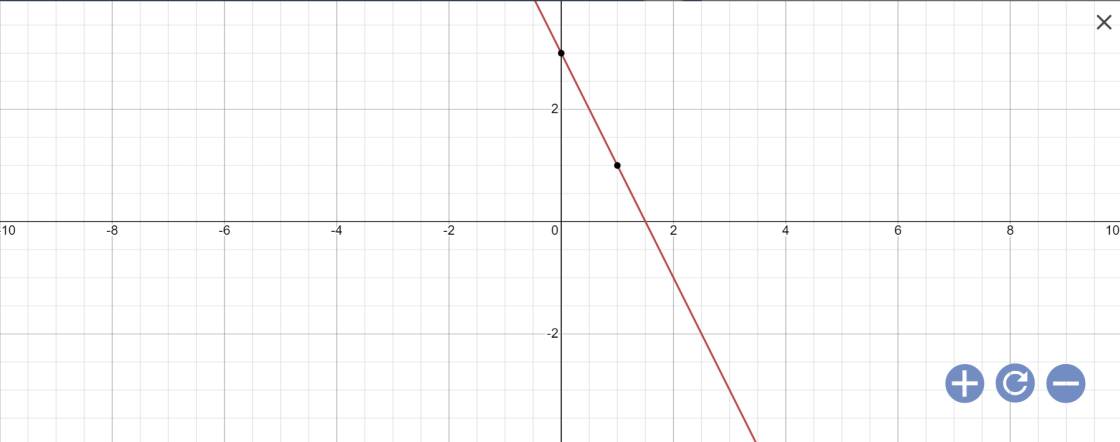
c: y=-2x+3

1+1=2

Vậy ? = 2

2+2=4

Vậy ??=4

3+3=6

Vậy ???=6

?+??+???=2+4+6=12

1+1=?

=> ?=2

2+2=??

=> ??=4

3+3=???

=> ???=6

Suy ra M=2+4+6=12

Lời giải:
Gọi tia sáng mặt trời tạo với mặt đất là $\alpha$. 

Ta có:
$\tan \alpha = \frac{7,5}{12}=\frac{5}{8}$

$\Rightarrow \alpha = 32^0$

Hình vẽ: