Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) ĐKXĐ: \(x^2-25\ne0\Leftrightarrow x^2\ne25\Leftrightarrow\left\{{}\begin{matrix}x\ne5\\x\ne-5\end{matrix}\right.\)
\(\dfrac{x^2-4x-5}{x^2-25}=0\)
\(\Leftrightarrow\dfrac{x^2-5x+x-5}{\left(x+5\right)\left(x-5\right)}=0\)
\(\Leftrightarrow\dfrac{x\left(x-5\right)+\left(x-5\right)}{\left(x+5\right)\left(x-5\right)}=0\)
\(\Leftrightarrow\dfrac{\left(x-5\right)\left(x+1\right)}{\left(x-5\right)\left(x+5\right)}=0\)
\(\Leftrightarrow\dfrac{x+1}{x+5}=0\)
\(\Leftrightarrow x+1=0\)
\(\Leftrightarrow x=-1\left(tm\right)\)
Vậy \(S=\left\{-1\right\}\)
b) ĐKXĐ: \(x-2\ne0\Leftrightarrow x\ne2\)
\(\dfrac{x^2-5x+6}{x-2}=1\)
\(\Leftrightarrow x^2-5x+6=x-2\)
\(\Leftrightarrow x^2-5x+6-x+2=0\)
\(\Leftrightarrow x^2-6x+8=0\)
\(\Leftrightarrow x^2-2x-4x+8=0\)
\(\Leftrightarrow\left(x^2-2x\right)-\left(4x-8\right)=0\)
\(\Leftrightarrow x\left(x-2\right)-4\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\left(ktm\right)\\x=4\left(tm\right)\end{matrix}\right.\)
Vậy \(S=\left\{4\right\}\)
c) ĐKXĐ: \(\left\{{}\begin{matrix}x\ne0\\x+8\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne0\\x\ne-8\end{matrix}\right.\)
\(\dfrac{x-2}{x+8}+\dfrac{1}{x}=\dfrac{8}{x\left(x+8\right)}\)
\(\Leftrightarrow\left(x-2\right)x+\left(x+8\right)=8\)
\(\Leftrightarrow x^2-2x+x+8=8\)
\(\Leftrightarrow x^2-x+8-8=0\)
\(\Leftrightarrow x^2-x=0\)
\(\Leftrightarrow x\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(ktm\right)\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\left(tkm\right)\\x=1\left(tm\right)\end{matrix}\right.\)
Vậy \(S=\left\{1\right\}\)

a) ĐKXĐ: Với mọi \(x\in R\)
\(\dfrac{15x-10}{x^2+2}=0\)
\(\Leftrightarrow15x-10=0\)
\(\Leftrightarrow15x=10\)
\(\Leftrightarrow x=\dfrac{2}{3}\) (nhận)
Vậy \(S=\left\{\dfrac{2}{3}\right\}\)
b) ĐKXĐ: \(x\ne0\)
\(\dfrac{6}{x}-1=\dfrac{2x-3}{3}\)
\(\Leftrightarrow3.6-3x=\left(2x-3\right)x\)
\(\Leftrightarrow18-3x=2x^2-3x\)
\(\Leftrightarrow2x^2=18\)
\(\Leftrightarrow x^2=9\)
\(\Leftrightarrow x=3\) (nhận) hoặc \(x=-3\) (nhận)
Vậy \(S=\left\{-3;3\right\}\)
c) ĐKXĐ: \(\left\{{}\begin{matrix}x+1\ne0\\x-1\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne-1\\x\ne1\end{matrix}\right.\)
\(\dfrac{3x-1}{x+1}=\dfrac{2x+1}{x-1}\)
\(\Leftrightarrow\left(3x-1\right)\left(x-1\right)=\left(2x+1\right)\left(x+1\right)\)
\(\Leftrightarrow3x^2-3x-x+1=2x^2+2x+x+1\)
\(\Leftrightarrow3x^2-4x+1-2x^2-2x-x-1\)
\(\Leftrightarrow x^2-7x=0\)
\(\Leftrightarrow x\left(x-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x-7=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\left(tm\right)\\x=7\left(tm\right)\end{matrix}\right.\)
Vậy \(S=\left\{0;7\right\}\)

a) ĐKXĐ:
\(\left\{{}\begin{matrix}2x-3\ne0\\2x-4\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}2x\ne3\\2x\ne4\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{3}{2}\\x\ne2\end{matrix}\right.\)
b) ĐKXĐ:
\(\left\{{}\begin{matrix}x-2\ne0\\x+3\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne2\\x\ne-3\end{matrix}\right.\)

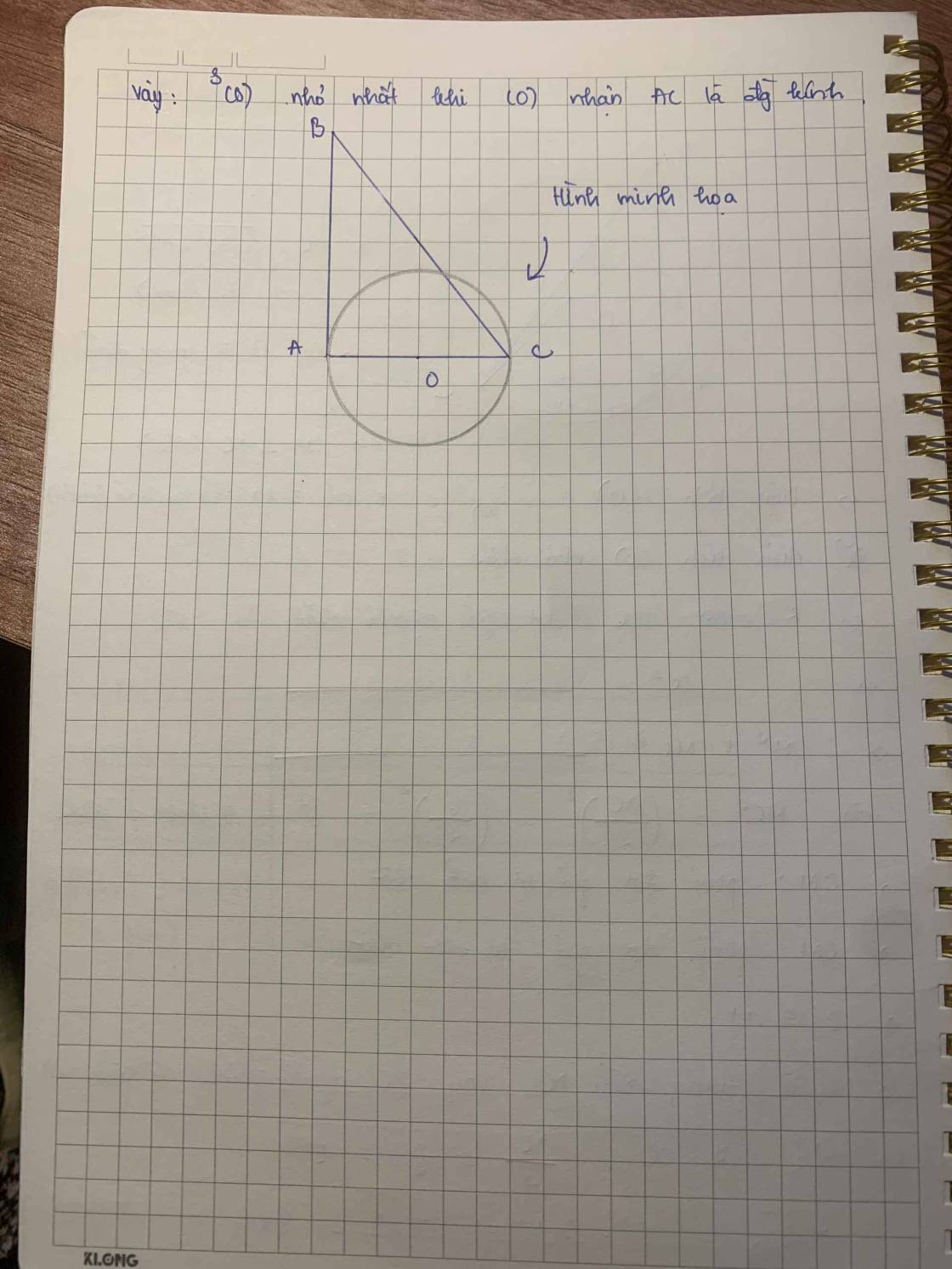
a) \(2x\left(3x-2\right)+\left(x+1\right)\left(3x-2\right)=0\)
\(\Leftrightarrow\left(3x-2\right)\left[2x+\left(x+1\right)\right]=0\)
\(\Leftrightarrow\left(3x-2\right)\left(2x+x+1\right)=0\)
\(\Leftrightarrow\left(3x-2\right)\left(3x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-2=0\\3x+1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=2\\3x=-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{1}{3}\end{matrix}\right.\)
Vậy \(S=\left\{-\dfrac{1}{3};\dfrac{2}{3}\right\}\)
b) \(\left(x-1\right)^2=\left(2x+3\right)^2\)
\(\Leftrightarrow\left(x-1\right)^2-\left(2x+3\right)^2=0\)
\(\Leftrightarrow\left(x-1+2x+3\right)\left(x-1-2x-3\right)=0\)
\(\Leftrightarrow\left(3x+2\right)\left(-x-4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+2=0\\-x-4=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x=-2\\-x=4\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{2}{3}\\x=-4\end{matrix}\right.\)
Vậy \(S=\left\{-4;-\dfrac{2}{3}\right\}\)
c) \(\left(2x+1\right)\left(x-1\right)+2=2x\)
\(\Leftrightarrow\left(2x+1\right)\left(x-1\right)+2-2x=0\)
\(\Leftrightarrow\left(2x+1\right)\left(x-1\right)-2\left(x-1\right)=0\)
\(\Leftrightarrow\left(x-1\right)\left[\left(2x+1\right)-2\right]=0\)
\(\Leftrightarrow\left(x-1\right)\left(2x+1-2\right)\)
\(\Leftrightarrow\left(x-1\right)\left(2x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2x-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\2x=1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=\dfrac{1}{2}\end{matrix}\right.\)
Vậy \(S=\left\{\dfrac{1}{2};1\right\}\)
d) \(x^2-x-12=0\)
\(\Leftrightarrow x^2-4x+3x-12=0\)
\(\left(x^2-4x\right)+\left(3x-12\right)=0\)
\(\Leftrightarrow x\left(x-4\right)+3\left(x-4\right)=0\)
\(\Leftrightarrow\left(x-4\right)\left(x+3\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-4=0\\x+3=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=-3\end{matrix}\right.\)
Vậy \(S=\left\{-3;4\right\}\)

a) \(\left(x-2\right)\left(2x+1\right)=0\)
\(x-2=0\) hoặc \(2x+1=0\)
*) \(x-2=0\)
\(x=2\)
*) \(2x+1=0\)
\(2x=-1\)
\(x=-\dfrac{1}{2}\)
Vậy \(S=\left\{-\dfrac{1}{2};2\right\}\)
b) \(\left(3x+4\right)\left(9-2x\right)=0\)
\(3x+4=0\) hoặc \(9-2x=0\)
*) \(3x+4=0\)
\(3x=-4\)
\(x=-\dfrac{4}{3}\)
*) \(9-2x=0\)
\(2x=9\)
\(x=\dfrac{9}{2}\)
Vậy \(S=\left\{-\dfrac{4}{3};\dfrac{9}{2}\right\}\)
c) \(\left(x+7\right)\left(\dfrac{x+5}{2}-\dfrac{4x}{3}\right)=0\)
\(\left(x+7\right)\left[3\left(x+5\right)-2.4x\right]=0\)
\(\left(x+7\right)\left(3x+15-8x\right)=0\)
\(\left(x+7\right)\left(-5x+15\right)=0\)
\(x+7=0\) hoặc \(-5x+15=0\)
*) \(x+7=0\)
\(x=-7\)
*) \(-5x+15=0\)
\(-5x=-15\)
\(x=\dfrac{-15}{-5}\)
\(x=3\)
Vậy \(S=\left\{-7;3\right\}\)
d) \(\left(x+3\right)\left(2x+3\right)\left(x-5\right)=0\)
\(x+3=0\) hoặc \(2x+3=0\) hoặc \(x-5=0\)
*) \(x+3=0\)
\(x=-3\)
*) \(2x+3=0\)
\(2x=-3\)
\(x=-\dfrac{3}{2}\)
*) \(x-5=0\)
\(x=5\)
Vậy \(S=\left\{-3;-\dfrac{3}{2};5\right\}\)

Câu 1:
a.
$25x^2-10x+1=0$
$\Leftrightarrow (5x-1)^2=0\Leftrightarrow 5x-1=0$
$\Leftrightarrow x=\frac{1}{5}$
b.
$9x^4+8x^2-1=0$
$\Leftrightarrow (9x^4-x^2)+(9x^2-1)=0$
$\Leftrightarrow x^2(9x^2-1)+(9x^2-1)=0$
$\Leftrightarrow (9x^2-1)(x^2+1)=0$
$\Leftrightarrow (3x-1)(3x+1)(x^2+1)=0$
\(\Leftrightarrow \left[\begin{matrix} 3x+1=0\\ 3x-1=0\\ x^2+1=0\end{matrix}\right.\Leftrightarrow \Leftrightarrow \left[\begin{matrix} x=\frac{-1}{3}(\text{chọn})\\ x=\frac{1}{3}(\text{chọn})\\ x^2=-1<0(\text{loại})\end{matrix}\right.\)
c.
\(\left\{\begin{matrix}\ 2x-3y=1\\ -x+5y=3\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix}\ 2x-3y=1\\ -2x+10y=6\end{matrix}\right.\)
$\Rightarrow (2x-3y)+(-2x+10y)=1+6$
$\Leftrightarrow 7y=7\Leftrightarrow y=1$
$x=5y-3=5-3=2$
Câu 3:
a. Bạn tự vẽ hình
b. PT hoành độ giao điểm $(P)$ và $(d)$:
$x^2=(2m+1)x+2$
$\Leftrightarrow x^2-(2m+1)x-2=0(*)$
Để $(d)$ cắt $(P)$ tại 2 điểm phân biệt $A(x_1,y_1), B(x_2,y_2)$ thì PT $(*)$ phải có 2 nghiệm phân biệt $x_1,x_2$
Điều này xảy ra khi: $\Delta=(2m+1)^2+8>0$
$\Leftrightarrow m\in\mathbb{R}$
Áp dụng định lý Viet:
\(\left\{\begin{matrix} x_1+x_2=2m+1\\ x_1x_2=-2\end{matrix}\right.\)
Khi đó:
$x_1^2+x_2^2=13$
$\Leftrightarrow (x_1+x_2)^2-2x_1x_2=13$
$\Leftrightarrow (2m+1)^2-2(-2)=13$
$\Leftrightarrow (2m+1)^2+4=13$
$\Leftrightarrow (2m+1)^3=9\Leftrightarrow 2m+1=\pm 3$
$\Leftrightarrow m=1$ hoặc $m=-2$ (tm)

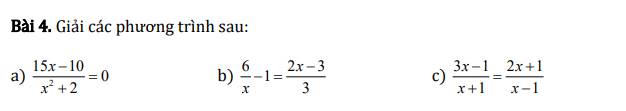

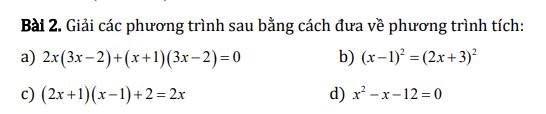



a) ĐKXĐ:
\(x-1\ne0\Leftrightarrow x\ne1\)
\(\dfrac{x+5}{3\left(x-1\right)}+1=\dfrac{3x+7}{5\left(x-1\right)}\)
\(\Leftrightarrow5\left(x+5\right)+15=3\left(3x+7\right)\)
\(\Leftrightarrow5x+25+15=9x+21\)
\(\Leftrightarrow5x-9x=21-25-15\)
\(\Leftrightarrow-4x=-19\)
\(\Leftrightarrow x=\dfrac{19}{4}\) (nhận)
Vậy \(S=\left\{\dfrac{19}{4}\right\}\)
b) ĐKXĐ: \(\left\{{}\begin{matrix}x+2\ne0\\x-2\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne-2\\x\ne2\end{matrix}\right.\)
\(\dfrac{1}{x+2}-\dfrac{1}{x-2}=\dfrac{3x-12}{x^2-4}\)
\(\Leftrightarrow x-2-x-2=3x-12\)
\(\Leftrightarrow-4=3x-12\)
\(\Leftrightarrow3x=-4+12\)
\(\Leftrightarrow3x=8\)
\(\Leftrightarrow x=\dfrac{8}{3}\) (nhận)
Vậy \(S=\left\{\dfrac{8}{3}\right\}\)
c) ĐKXĐ: \(\left\{{}\begin{matrix}x-1\ne0\\x+3\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x\ne1\\x\ne-3\end{matrix}\right.\)
\(\dfrac{3x-1}{x-1}-\dfrac{2x+5}{x+3}-\dfrac{8}{x^2+2x-3}=1\)
\(\Leftrightarrow\left(3x-1\right)\left(x+3\right)-\left(2x+5\right)\left(x-1\right)-8=x^2+2x-3\)
\(\Leftrightarrow3x^2+9x-x-3-2x^2+2x-5x+5-8=x^2+2x-3\)
\(\Leftrightarrow x^2+5x-6=x^2+2x-3\)
\(\Leftrightarrow x^2+5x-x^2-2x=-3+6\)
\(\Leftrightarrow3x=3\)
\(\Leftrightarrow x=1\) (loại)
Vậy \(S=\varnothing\)
d) ĐKXĐ: Với mọi \(x\in R\)
\(\dfrac{1}{x^2+x+1}-\dfrac{1}{x^2-x+1}=\dfrac{1-2x}{x^4+x^2+1}\)
\(\Leftrightarrow x^2-x+1-\left(x^2+x+1\right)=1-2x\)
\(\Leftrightarrow x^2-x+1-x^2-x-1=1-2x\)
\(\Leftrightarrow-2x=1-2x\)
\(\Leftrightarrow-2x+2x=1\)
\(\Leftrightarrow0x=1\) (vô lý)
Vậy \(S=\varnothing\)