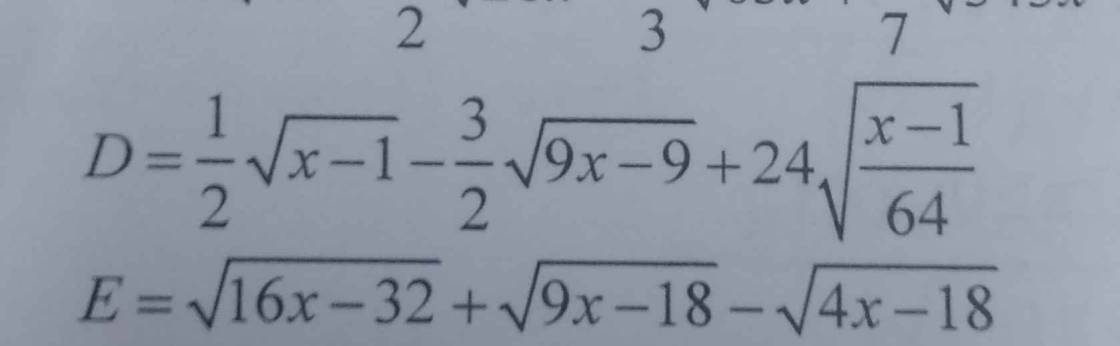hình lỗi rồi

Hình đâu ạ?

\(\dfrac{\sqrt{2}+\sqrt{3}+\sqrt{6}+\sqrt{8}+4}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)

\(=\dfrac{\sqrt{2}+\sqrt{3}+2+2+\sqrt{6}+\sqrt{8}}{\sqrt{2}+\sqrt{3}+\sqrt{4}}\)

\(=\dfrac{\left(\sqrt{2}+\sqrt{3}+\sqrt{4}\right)\left(1+\sqrt{2}\right)}{\sqrt{2}+\sqrt{3}+\sqrt{4}}=1+\sqrt{2}\)

Lời giải:

Giả sử hai người thợ làm một mình xong việc trong lần lượt là $a$ và $b$ giờ.

Trong 1 giờ người 1 làm được $\frac{1}{a}$ công việc, người 2 làm được $\frac{1}{b}$ công việc.

Theo bài ra ta có:

\(\left\{\begin{matrix} \frac{16}{a}+\frac{16}{b}=1\\ \frac{3}{a}+\frac{6}{b}=\frac{1}{4}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} \frac{1}{a}=\frac{1}{24}\\ \frac{1}{b}=\frac{1}{48}\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} a=24\\ b=48\end{matrix}\right.\) (giờ)

Lời giải:

$D=\frac{1}{2}\sqrt{x-1}-\frac{3}{2}\sqrt{9(x-1)}+24\sqrt{\frac{1}{64}(x-1)}$

$=\frac{1}{2}\sqrt{x-1}-\frac{3}{2}.3\sqrt{x-1}+24.\frac{1}{8}\sqrt{x-1}$

$=\frac{1}{2}\sqrt{x-1}-\frac{9}{2}\sqrt{x-1}+3\sqrt{x-1}$

$=(\frac{1}{2}-\frac{9}{2}+3)\sqrt{x-1}=-\sqrt{x-1}$

---------------

Sửa: $4x-18\to 4x-8$

$E=\sqrt{16(x-2)}+\sqrt{9(x-2)}-\sqrt{4(x-2)}$

$=4\sqrt{x-2}+3\sqrt{x-2}-2\sqrt{x-2}$

$=(4+3-2)\sqrt{x-2}=5\sqrt{x-2}$

\(D=\dfrac{1}{2}\sqrt{x-1}-\dfrac{3}{2}\sqrt{9x-9}+24\sqrt{\dfrac{x-1}{64}}\)

\(D=\dfrac{1}{2}\sqrt{x-1}-\dfrac{3}{2}\sqrt{9\left(x-1\right)}+24\dfrac{\sqrt{x-1}}{8}\)

\(D=\dfrac{1}{2}\sqrt{x-1}-\dfrac{9}{2}\sqrt{x-1}+192\sqrt{x-1}\)

\(D=\sqrt{x-1}\left(\dfrac{1}{2}-\dfrac{9}{2}+3\right)\)

\(D=-\sqrt{x-1}\)

\(E=\sqrt{16x-32}+\sqrt{9x-18}-\sqrt{4x-8}\)

\(E=\sqrt{16\left(x-2\right)}+\sqrt{9\left(x-2\right)}-\sqrt{4\left(x-2\right)}\)

\(E=4\sqrt{x-2}+3\sqrt{x-2}-2\sqrt{x-2}\)

\(E=\sqrt{x-2}\left(4+3-2\right)\)

\(E=5\sqrt{x-2}\)

Gọi giá mở cửa của hãng taxi là x(đồng)

(ĐIều kiện: x>0)

Giá mỗi km ở mức 2 là x+300(đồng)

Giá mỗi km ở mức 3 là x+300-500=x-200(đồng)

Giá mỗi km ở mức 4 là x-200-800=x-1000(đồng)

800m=0,8km

Số tiền phải trả ở mức 1 là 0,8x(đồng)

Số km đi ở mức 2 là 15-0,8=14,2

Số tiền phải trả ở mức 2 là 14,2(x+300)(đồng)

Số tiền phải trả ở mức 3 là 15(x-200)(đồng)

Số km đi ở mức 4 là: 50-30=20(km)

Số tiền phải trả ở mức 4 là 20(x-1000)(đồng)

Tổng số tiền phải trả là 481260 đồng nên ta có:

0,8x+14,2(x+300)+15(x-200)+20(x-1000)=481260

=>0,8x+14,2x+4260+15x-3000+20x-20000=481260

=>50x-18740=481260

=>50x=500000

=>x=10000(nhận)

Vậy: Giá mở cửa của taxi là 10000 đồng

Bạn nên viết đề bằng công thức toán (biểu tượng $\sum$ góc trái khung soạn thảo) để mọi người hiểu đề và hỗ trợ bạn tốt hơn nhé.

a: Xét tứ giác ABOC có \(\widehat{OBA}+\widehat{OCA}=90^0+90^0=180^0\)

nên ABOC là tứ giác nội tiếp

b: Xét (O) có

\(\widehat{ABE}\) là góc tạo bởi tiếp tuyến BA và dây cung BE

\(\widehat{BFE}\) là góc nội tiếp chắn cung BE

Do đó: \(\widehat{ABE}=\widehat{BFE}\)

Xét ΔABE và ΔAFB có

\(\widehat{ABE}=\widehat{AFB}\)

\(\widehat{BAE}\) chung

Do đó: ΔABE~ΔAFB

=>\(\dfrac{AB}{AF}=\dfrac{AE}{AB}\)

=>\(AB^2=AF\cdot AE\)

c: Xét (O) có

AB,AC là các tiếp tuyến

Do đó: AB=AC

=>A nằm trên đường trung trực của BC(1)

ta có: OB=OC

=>O nằm trên đường trung trực của BC(2)

Từ (1),(2) suy ra OA là đường trung trực của BC

=>OA\(\perp\)BC tại X

ΔOEF cân tại O

mà OD là đường trung tuyến

nên OD\(\perp\)FE tại D

Xét ΔAXK vuông tại X và ΔADO vuông tại D có

\(\widehat{XAK}\) chung

Do đó: ΔAXK~ΔADO

=>\(\dfrac{AX}{AD}=\dfrac{AK}{AO}\)

=>\(AX\cdot AO=AD\cdot AK\)

Xét ΔABO vuông tại B có BX là đường cao

nên \(AX\cdot AO=AB^2\)

=>\(AE\cdot AF=AK\cdot AD\)

Ta có: \(\widehat{ADO}=\widehat{ABO}=\widehat{ACO}=90^0\)

=>A,D,B,C,O cùng thuộc đường tròn đường kính AO

Gọi độ dài quãng đường AB là x(km)

(Điều kiện: x>0)

Thời gian ô tô đi từ A đến B là \(\dfrac{x}{50}\left(giờ\right)\)

Thời gian ô tô đi từ B về A là \(\dfrac{x}{60}\left(giờ\right)\)

Tổng thời gian đi và về là:

4h-20p=3h40p=11/3(giờ)

Do đó, ta có phương trình:

\(\dfrac{x}{50}+\dfrac{x}{60}=\dfrac{11}{3}\)

=>\(\dfrac{11x}{300}=\dfrac{11}{3}\)

=>\(\dfrac{x}{300}=\dfrac{1}{3}\)

=>x=100(nhận)

vậy: Độ dài quãng đường AB là 100km