Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

y + y : 0,25 + 222 - y : 0,5 = 2022
y + y : 1/4 + 222 - y : 1/2 = 2022
y x 1 + y x 4 - y x 2 = 2022 - 222
y x ( 1 + 4 - 2 ) = 1800
y x 3 = 1800
y = 1800 : 3 = 600
2023 x 2022 - 2022 x 2021 + 2022 x 1 + 2022 x 7
= 2022 x (2023 - 2021 + 1 + 7 )
= 2022 x 10
= 20220
y + y : 0,25 + 222 - y : 0,5 = 2022
y + y : 1/4 + 222 - y : 1/2 = 2022
y x 1 + y x 4 - y x 2 = 2022 - 222
y x ( 1 + 4 - 2 ) = 1800
y x 3 = 1800
y = 1800 : 3 = 600
2023 x 2022 - 2022 x 2021 + 2022 x 1 + 2022 x 7
= 2022 x (2023 - 2021 + 1 + 7 )
= 2022 x 10
= 20220

b) \(B=\dfrac{1}{\sqrt{x}+1}+\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{2}{x-1}\left(x\ge0,x\ne1\right)\\ =\dfrac{1}{\sqrt{x}+1}+\dfrac{\sqrt{x}}{\sqrt{x}-1}+\dfrac{2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{\sqrt{x}-1+\sqrt{x}\left(\sqrt{x}+1\right)+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{\sqrt{x}-1+x+\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ =\dfrac{x+2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\\ \)
\(=\dfrac{\left(\sqrt{x}+1\right)^2}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
c)
\(AB\le8\Leftrightarrow\dfrac{4\sqrt{x}}{x-1}.\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\le8\\ \Leftrightarrow\dfrac{4\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}.\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\le8\\ \Leftrightarrow\dfrac{4\sqrt{x}}{\left(\sqrt{x}-1\right)^2}\le8\\ \Leftrightarrow4\sqrt{x}\le8\left(x-2\sqrt{x}+1\right)\\ \) ( Nhân cả 2 vế BPT cho \(\left(\sqrt{x}-1\right)^2>0\) )
\(\Leftrightarrow8x-16\sqrt{x}+8\ge4\sqrt{x}\\ \Leftrightarrow8x-20\sqrt{x}+8\ge0\\ \Leftrightarrow2x-5\sqrt{x}+2\ge0\\ \)
\(\Leftrightarrow\left(2x-4\sqrt{x}\right)-\left(\sqrt{x}-2\right)\ge0\\ \Leftrightarrow2\sqrt{x}\left(\sqrt{x}-2\right)-\left(\sqrt{x}-2\right)\ge0\\ \Leftrightarrow\left(\sqrt{x}-2\right)\left(2\sqrt{x}-1\right)\ge0\\ \)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\sqrt{x}-2\ge0\\2\sqrt{x}-1\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}\sqrt{x}-2\le0\\2\sqrt{x}-1\le0\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\sqrt{x}\ge2\\\sqrt{x}\ge\dfrac{1}{2}\end{matrix}\right.\\\left\{{}\begin{matrix}\sqrt{x}\le2\\\sqrt{x}\le\dfrac{1}{2}\end{matrix}\right.\end{matrix}\right.\\ \)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x\ge4\\x\ge\dfrac{1}{4}\end{matrix}\right.\\\left\{{}\begin{matrix}x\le4\\x\le\dfrac{1}{4}\end{matrix}\right.\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x\ge4\\x\le\dfrac{1}{4}\end{matrix}\right.\)
Kết hợp ĐK: \(x\ge0,x\ne1\)
Kết luận: \(x\ge4\) hoặc \(0\le x\le\dfrac{1}{4}\) thì \(AB\le8\)
Lời giải:
ĐK: $x\geq 0; x\neq 1$
$AB=\frac{4\sqrt{x}}{(\sqrt{x}-1)^2}\leq 8$
$\Rightarrow 4\sqrt{x}\leq 8(\sqrt{x}-1)^2$
$\Leftrightarrow \sqrt{x}\leq 2(\sqrt{x}-1)^2$
$\Leftrightarrow \sqrt{x}\leq 2(x-2\sqrt{x}+1)$
$\Leftrightarrow 2x-5\sqrt{x}+2\geq 0$
$\Leftrightarrow (\sqrt{x}-2)(2\sqrt{x}-1)\geq 0$
$\Leftrightarrow \sqrt{x}\geq 2$ hoặc $\sqrt{x}\leq \frac{1}{2}$
$\Leftrightarrow x\geq 4$ hoặc $0\leq x\leq \frac{1}{4}$
Kết hợp đkxđ suy ra $x\geq 4$ hoặc $0\leq x\leq \frac{1}{4}$

Diện tích xung quanh là:
\(\left(25+12\right)\cdot2\cdot2,5=5\cdot37=185\left(m^2\right)\)
Diện tích cần lát gạch là:
\(185+25\cdot12=185+300=485\left(m^2\right)\)=4850000(cm2)
Diện tích 1 viên gạch là 502=2500(cm2)
Số viên gạch cần dùng là:
4850000:2500=1940(viên)
=>Chọn D

\(B=\dfrac{2\sqrt{x}-3}{\sqrt{x}-1}+\dfrac{3-\sqrt{x}}{x-1}\)
\(=\dfrac{2\sqrt{x}-3}{\sqrt{x}-1}+\dfrac{3-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(2\sqrt{x}-3\right)\left(\sqrt{x}+1\right)+3-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{2x+2\sqrt{x}-3\sqrt{x}-3+3-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{2x-2\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{2\sqrt{x}}{\sqrt{x}+1}\)

`300 + 600 + 400 + 700 + 545 + 455`
`= (300 + 700) + (600 + 400) + (545 + 455)`
`= 1000 + 1000 + 1000`
`=3000`

Câu 1: B
Câu 2: C
Câu 3: C
Câu 4: A
Câu 5: D
Câu 6: B
Câu 7: D
Câu 8: A
Câu 9: D
Câu 10: D

\(B=\dfrac{2x-3}{\sqrt{x}-1}+\dfrac{3-\sqrt{x}}{x-1}\)
\(=\dfrac{2x-3}{\sqrt{x}-1}+\dfrac{3-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(2x-3\right)\left(\sqrt{x}+1\right)+3-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{2x\sqrt{x}+2x-3\sqrt{x}-3+3-\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{2x\sqrt{x}+2x-4\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{2\sqrt{x}\left(x+\sqrt{x}-2\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{2\sqrt{x}\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}=\dfrac{2\sqrt{x}\left(\sqrt{x}+2\right)}{\sqrt{x}+1}=\dfrac{2x+4\sqrt{x}}{\sqrt{x}+1}\)

a: \(\text{Δ}=\left(-3\right)^2-4\left(-m^2+2\right)\)
\(=9+4m^2-8=4m^2+1>0\forall m\)
=>Phương trình luôn có hai nghiệm phân biệt
b:
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=3\\x_1x_2=\dfrac{c}{a}=-m^2+2\end{matrix}\right.\)
\(x_1>x_2\)
=>\(x_1-x_2>0\)
\(\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2\)
\(=3^2-4\left(-m^2+2\right)\)
\(=9+4m^2-8=4m^2+1\)
=>\(x_1-x_2=\sqrt{4m^2+1}\)
\(A=x_1^2-x_2^2+5\left(x_1+x_2\right)\)
\(=\left(x_1-x_2\right)\left(x_1+x_2\right)+5\left(x_1+x_2\right)\)
\(=3\sqrt{4m^2+1}+15>=3\cdot1+15=18\forall m\)
Dấu '=' xảy ra khi m=0
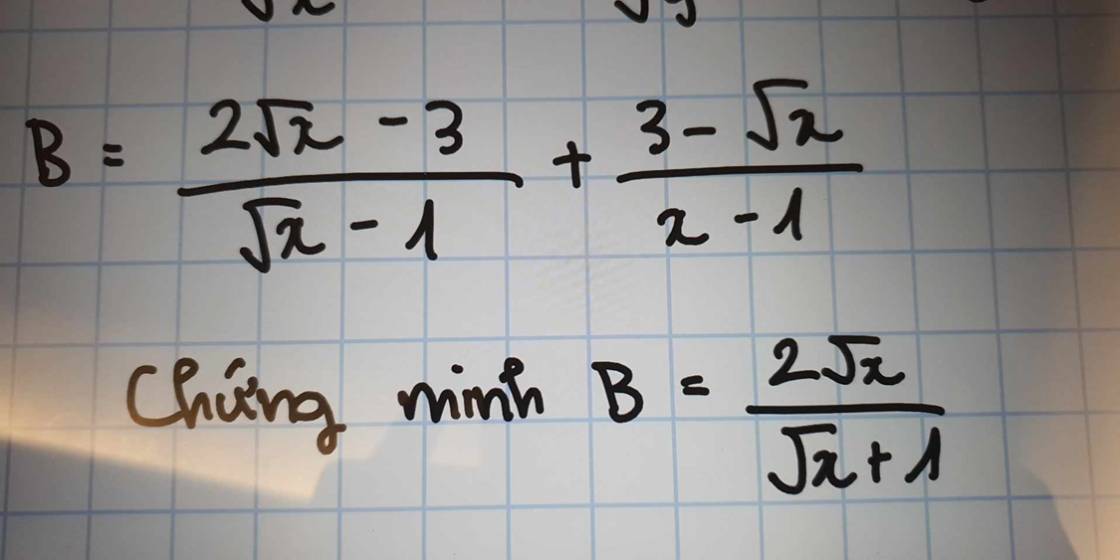

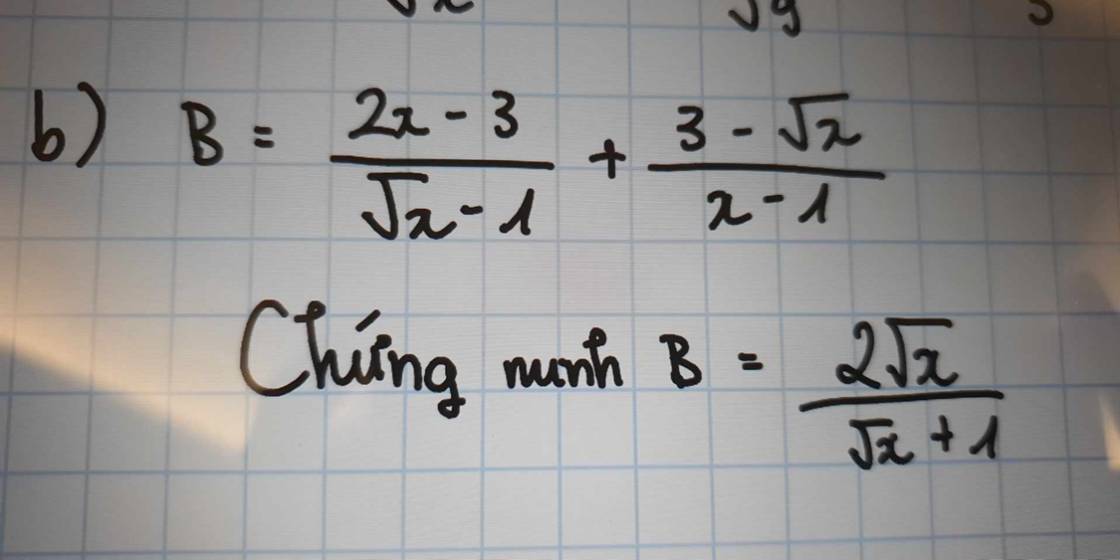 Bạn nào biết giải bài này không ạ giúp mình nhé. Mình cảm ơn nhiều
Bạn nào biết giải bài này không ạ giúp mình nhé. Mình cảm ơn nhiều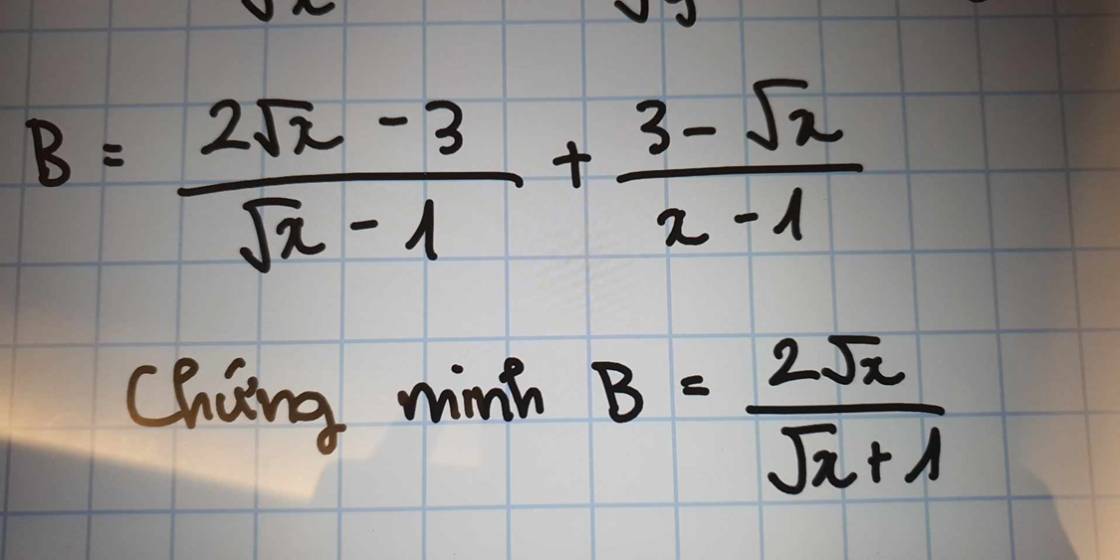
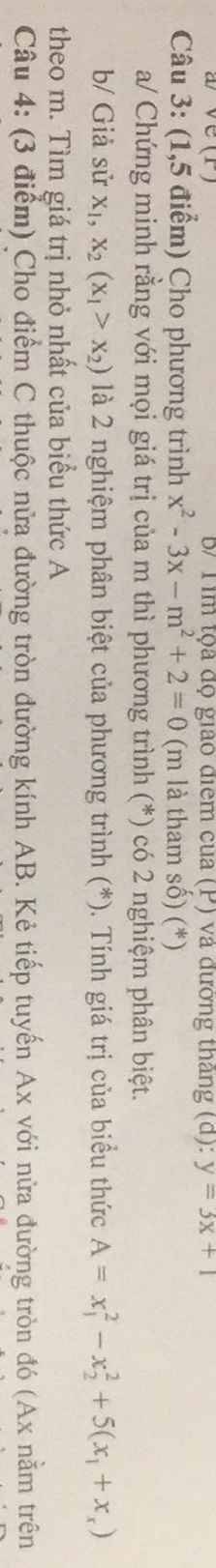
Tỉ số giữa số dầu ở thùng 1 và thùng 3 là:
\(1,5\times\dfrac{1}{3}=\dfrac{1}{2}\)
Tổng số dầu ở 3 thùng là 200x3=600(lít)
Số dầu ở thùng 3 là:
\(600:\left(\dfrac{1}{2}+1,5+1\right)=600:3=200\left(lít\right)\)
Số dầu ở thùng 2 là:
\(200\times1,5=300\left(lít\right)\)
Số dầu ở thùng 1 là:
\(300\times\dfrac{1}{3}=100\left(lít\right)\)
Tỉ số giữa số dầu ở thùng 1 và thùng 3 là:
1,5×13=121,5×31=21
Tổng số dầu ở 3 thùng là 200x3=600(lít)
Số dầu ở thùng 3 là:
600:(12+1,5+1)=600:3=200(𝑙ıˊ𝑡)600:(21+1,5+1)=600:3=200(lıˊt)
Số dầu ở thùng 2 là:
200×1,5=300(𝑙ıˊ𝑡)200×1,5=300(lıˊt)
Số dầu ở thùng 1 là:
300×13=100(𝑙ıˊ𝑡)300×31=100(lıˊt)