
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(x^4+2x^2+1=\left(x^2\right)^2+2x^2+1=\left(x^2+1\right)^2\)

a/
$A=x^2-4x+10=(x^2-4x+4)+6=(x-2)^2+6$
Ta thấy:
$(x-2)^2\geq 0$ với mọi $x\in\mathbb{R}$
$\Rightarrow A=(x-2)^2+6\geq 6>0$ với mọi $x\in\mathbb{R}$
$\Rightarrow A$ luôn có giá trị dương với mọi giá trị $x$.
a/
$B=2x^2-2x+3=x^2+(x^2-2x+1)+2=x^2+(x-1)^2+2$
Ta thấy:
$x^2\geq 0; (x-1)^2\geq 0$ với mọi $x\in\mathbb{R}$
$\Rightarrow B=x^2+(x-1)^2+2\geq 2>0$ với mọi $x\in\mathbb{R}$
$\Rightarrow B$ luôn có giá trị dương với mọi giá trị $x$.

Bài 22:
a: Diện tích 1 ô trồng hoa là \(a^2\left(m^2\right)\)
Diện tích trồng hoa là \(4\cdot a^2\left(m^2\right)\)
Diện tích đất trồng rau là: \(20^2-4a^2=400-4a^2\left(m^2\right)\)
b: Diện tích đất trồng hoa bằng diện tích đất trồng rau
=>\(4a^2=400-4a^2\)
=>\(8a^2=400\)
=>\(a^2=50\)
=>\(a=5\sqrt{2}\)
c:
Số tiền lãi khi trồng hoa là: \(20000\cdot4a^2=80000a^2\left(đồng\right)=80a^2\left(nghìnđồng\right)\)
Số tiền lãi khi trồng rau là: \(15\cdot\left(400-4a^2\right)=6000-60a^2\)(nghìn đồng)
Số tiền lãi trồng hoa bằng 3/4 số tiền lãi trồng rau nên ta có:
\(80a^2=\dfrac{3}{4}\left(6000-60a^2\right)\)
=>\(80a^2=4500-45a^2\)
=>\(125a^2=4500\)
=>\(a^2=36\)
=>Diện tích đất trồng hoa là \(4a^2=144\left(m^2\right)\)

a: \(A=2n^2+n-3\)
\(=2n^2+3n-2n-3\)
\(=n\left(2n+3\right)-\left(2n+3\right)=\left(2n+3\right)\left(n-1\right)\)
Nếu n=0 thì \(A=\left(2\cdot0+3\right)\left(0-1\right)=-3< 0\)
=>Loại
Nếu n=1 thì \(A=\left(2\cdot1+3\right)\left(1-1\right)=0\)
=>Loại
Nếu n=2 thì \(A=\left(2\cdot2+3\right)\left(2-1\right)=7\) là số nguyên tố
=>Nhận
Khi n>2 thì \(A=\left(2n+3\right)\left(n-1\right)\) là tích của 2 số tự nhiên lớn hơn 1
=>A không phải là số nguyên tố
=>Loại
b: \(B=n^4+n^2+1=n^4+2n^2+1-n^2\)
\(=\left(n^2+1\right)^2-n^2=\left(n^2-n+1\right)\left(n^2+n+1\right)\)
Khi n=0 thì \(B=\left(0^2-0+1\right)\left(0^2+0+1\right)=1\)
=>Loại
Khi n=1 thì \(B=\left(1^2-1+1\right)\left(1^2+1+1\right)=3\) là số nguyên tố
=>Nhận
Khi n>1 thì \(B=\left(n^2-n+1\right)\left(n^2+n+1\right)\) là tích của hai số tự nhiên lớn hơn 1
=>Loại

`#3107.101107`
`(a + b + c)^2 = a^2 + b^2 + c^2`
`\Rightarrow (a + b + c)^2 - (a^2 + b^2 + c^2) = 0`
`\Rightarrow a^2 + b^2 + c^2 + 2ab + 2bc + 2ca - a^2 - b^2 - c^2 = 0`
`\Rightarrow 2ab + 2bc + 2ca = 0`
`\Rightarrow 2(ab + bc + ca) = 0`
`\Rightarrow ab + bc + ca = 0`
\(\Rightarrow\dfrac{ab+bc+ca}{abc}=0\\ \Rightarrow\dfrac{ab}{abc}+\dfrac{bc}{abc}+\dfrac{ca}{abc}=0\\ \Rightarrow\dfrac{1}{c}+\dfrac{1}{a}+\dfrac{1}{b}=0\)
Đặt \(x=\dfrac{1}{a};y=\dfrac{1}{b};z=\dfrac{1}{c}\)
`=> x + y + z = 0`
`=> x + y = -z` (*)
`=> (x + y)^3 = -(z)^3`
`=> x^3 + y^3 + 3xy(x + y) = -z^3`
Thay (*) vào bt
`=> x^3 + y^3 + z^3 + 3xy(-z) = 0`
`=> x^3 + y^3 + z^3 - 3xyz = 0`
`=> x^3 + y^3 + z^3 = 3xyz`
`=>`\(\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}=\dfrac{3}{abc}\left(\text{đpcm}\right).\)

\(-6x^2+23x-20\)
\(=-6x^2+15x+8x-20\)
\(=-3x\left(2x-5\right)+4\left(2x-5\right)=\left(2x-5\right)\left(-3x+4\right)\)

Sửa đề: \(3x^2-6xy+3y^2-12z^2\)
\(=3\left(x^2-2xy+y^2-4z^2\right)\)
\(=3\left[\left(x-y\right)^2-\left(2z\right)^2\right]\)
\(=3\left(x-y-2z\right)\left(x-y+2z\right)\)

a) Vì tứ giác ABCD là hình vuông
nên \(\left\{{}\begin{matrix}AB=BC=CD=DA\\\widehat{ABC}=\widehat{BCD}=\widehat{CDA}=\widehat{DAB}=90^{\circ}\end{matrix}\right.\) (t/c)
Mà: \(\left\{{}\begin{matrix}MA=MB=\dfrac{AB}{2}\\NB=NC=\dfrac{BC}{2}\end{matrix}\right.\) (do M, N lần lượt là trung điểm của AB, BC)
Do đó: \(MA=MB=NB=NC\)
Xét \(\Delta BCM\) và \(\Delta CDN\) có: \(\left\{{}\begin{matrix}MB=NC\left(cmt\right)\\\widehat{MBC}=\widehat{NCD}\left(=90^{\circ}\right)\\BC=CD\left(cmt\right)\end{matrix}\right.\)
\(\Rightarrow\Delta BCM=\Delta CDN\left(c.g.c\right)\)
\(\Rightarrow\widehat{BCM}=\widehat{CDN}\) (hai góc tương ứng)
Mà: \(\widehat{BCM}+\widehat{MCD}=\widehat{BCD}=90^{\circ}\) (hai góc kề phụ)
nên \(\widehat{CDN}+\widehat{MCD}=90^{\circ}\)
hay \(\widehat{CDH}+\widehat{HCD}=90^{\circ}\) (vì \(CM\cap DN=\left\{H\right\}\))
\(\Rightarrow\widehat{CHD}=90^{\circ}\Rightarrow CM\perp DN\) (đpcm)
b)
+, Gọi F là trung điểm của CD, G là giao điểm của AF với DH.
Xét \(\Delta DHC\) vuông tại H có: F là trung điểm của cạnh huyền CD
\(\Rightarrow HF=\dfrac{1}{2}CD=FD=FC\) (đli)
\(\Rightarrow F\) nằm trên đường trung trực của đoạn \(HD\) (1)
Vì F là trung điểm CD nên \(FC=FD=\dfrac{CD}{2}\)
Mà \(CD=AB;AM=BM=\dfrac{AB}{2}\left(cmt\right)\)
Do đó: \(FC=AM\)
Lại có: \(AB//CD\) (vì ABCD là hình vuông)
\(\Rightarrow AM//FC\) (vì \(M\in AB;F\in CD\))
Xét tứ giác AMCF có: \(\begin{cases} AM=FC(cmt)\\ AM//FC(cmt) \end{cases} \)
\(\Rightarrow\) Tứ giác AMCF là hình bình hành (t/c)
\(\Rightarrow AF//CM\) (t/c) \(\Rightarrow GF//HC\) (vì \(G\in AF;H\in CM\))
Xét \(\Delta DHC\) có: \(\begin{cases} F\text{ là trung điểm của CD }(cmt)\\ FG//HC\text{ }(cmt) \end{cases} \)
\(\Rightarrow G\) là trung điểm của DH (đli) (2)
Từ (1), (2) \(\Rightarrow FG\) là đường trung trực của đoạn DH
Mà \(A\in FG\Rightarrow\) A nằm trên đường trung trực của đoạn DH
\(\Rightarrow AD=AH\) (t/c) (*)
+, CMTT, ta cũng có: \(EH=EC\) (**)
Từ (*) và (**) \(\Rightarrow AD+EC=AH+EH=AE\) (vì \(H\in AE\)) (đpcm)
$Toru$
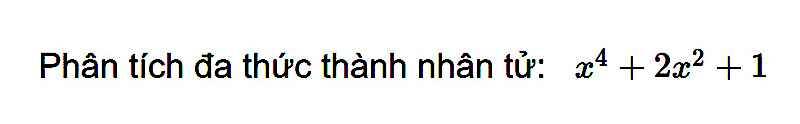


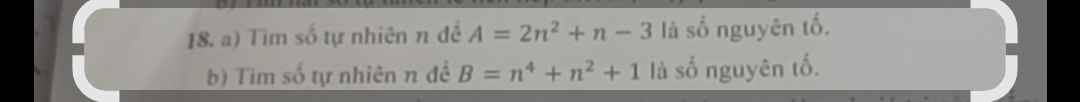
làm bài nào cx dc.