
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Ta có:
\(\widehat{ADE}=\widehat{ABC}\left(=45^o\right)\)
Mà hai góc này ở vị trí đồng vị
=> DE//BC
b) Ta có:
\(\widehat{FEC}=\widehat{ECB}\left(gt\right)\)
Mà hai góc này ở vị trí so le trong
=> EF//BC
c) Ta có: DE//BC
=> \(\widehat{DEC}+\widehat{ECB}=180^o\) (trong cùng phía)
Mà: \(\widehat{FEC}=\widehat{ECB}\left(gt\right)\)
\(=>\widehat{FEC}+\widehat{ECB}=180^o\)
\(=>\widehat{DEF}\) là góc bẹt
=> D, E, F thẳng hàng

a) Ta có:
\(\widehat{MAB}=\widehat{ABC}\left(=55^o\right)\)
Mà hai góc này ở vị trí so le trong
=> AM//BC
b) Ta có:
\(\widehat{NAC}=\widehat{ACB}\left(=40^o\right)\)
Mà hai góc này ở vị trí so le trong
=> AN//BC
c) Xét tam giác ABC có:
\(\widehat{BAC}+\widehat{ABC}+\widehat{ACB}=180^o\\ =>\widehat{BAC}=180^o-\widehat{ABC}-\widehat{ACB}\\ =>\widehat{BAC}=180^o-55^o-40^o=85^o\)
\(\widehat{MAB}+\widehat{BAC}+\widehat{NAC}=55^o+85^o+40^o=180^o\)
=> \(\widehat{MAN}\) là góc bẹt => M, A, N thẳng hàng

\(\left(8+2\dfrac{1}{3}-\dfrac{3}{5}\right):\left(5-\dfrac{1}{4}-\dfrac{5}{8}\right)\\ =\left(8+2+\dfrac{1}{3}-\dfrac{3}{5}\right):\left(5-\dfrac{2}{8}-\dfrac{5}{8}\right)\\ =\left(10+\dfrac{1}{3}-\dfrac{3}{5}\right):\left(5-\dfrac{7}{8}\right)\\ =\left(\dfrac{150}{15}+\dfrac{5}{15}-\dfrac{9}{15}\right):\left(\dfrac{40}{8}-\dfrac{7}{8}\right)\\ =\dfrac{146}{15}:\dfrac{33}{8}\\ =\dfrac{146}{15}\cdot\dfrac{8}{33}\\ =\dfrac{1168}{495}\)

\(f\left(x\right)+g\left(x\right)=x^2h\left(x\right)\)
\(2x^3-3x^2+3x+1+g\left(x\right)=x^2\left(2x+1\right)\)
\(g\left(x\right)=2x^3+x^2-2x^3+3x^2-3x-1=4x^2-3x-1\)
chọn C
`#3107.101107`
Ta có:
`f(x) + g(x) = x^2h(x)`
`\Rightarrow g(x) = x^2h(x) - f(x)`
`g(x) = x^2 * (2x + 1) - (2x^3 - 3x^2 + 3x + 1)`
`= 2x^3 + x^2 - 2x^3 + 3x^2 - 3x - 1`
`= 4x^2 - 3x - 1`
Chọn C.

Xét đường thẳng BC, có AH, AB lần lượt là đường vuông góc và đường xiên kẻ từ A đến BC. Do đó \(AH< AB\).
Chứng minh tương tự, ta được \(BK< BC\) và \(CL< CA\)
Cộng theo vế 3 BĐT vừa tìm được, ta có:
\(AH+BK+CL< AB+BC+CA\) (đpcm)

\(A=\dfrac{4^5\cdot9^4-2\cdot6^9}{2^{10}\cdot3^8+6^8\cdot20}\\ =\dfrac{\left(2^2\right)^5\cdot\left(3^2\right)^4-2\cdot2^9\cdot3^9}{2^{10}\cdot3^8+2^8\cdot3^8\cdot20}\\ =\dfrac{2^{10}\cdot3^8-2^{10}\cdot3^9}{2^{10}\cdot3^8+2^8\cdot3^8\cdot2^2\cdot5}\\ =\dfrac{2^{10}\cdot3^8-2^{10}\cdot3^9}{2^{10}\cdot3^8+2^{10}\cdot3^8\cdot5}\\ =\dfrac{2^{10}\cdot3^8\cdot\left(1-3\right)}{2^{10}\cdot3^8\cdot\left(1+5\right)}\\ =\dfrac{-2}{6}\\ =-\dfrac{1}{3}\)

\(B=4\cdot2^7:\left(3^{11}\cdot\dfrac{1}{9}\right)\\ =4\cdot2^7:\left(3^{11}\cdot\dfrac{1}{3^2}\right)\\ =4\cdot2^7:\dfrac{3^{11}}{3^2}\\ =4\cdot2^7:3^9\\ =\dfrac{2^2\cdot2^7}{3^9}\\ =\dfrac{2^9}{3^9}\\ =\left(\dfrac{2}{3}\right)^9\)

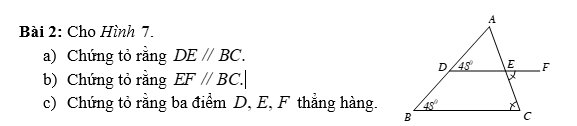
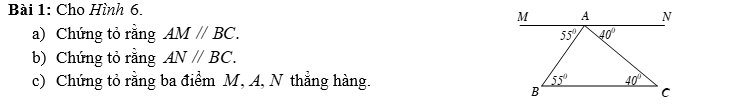
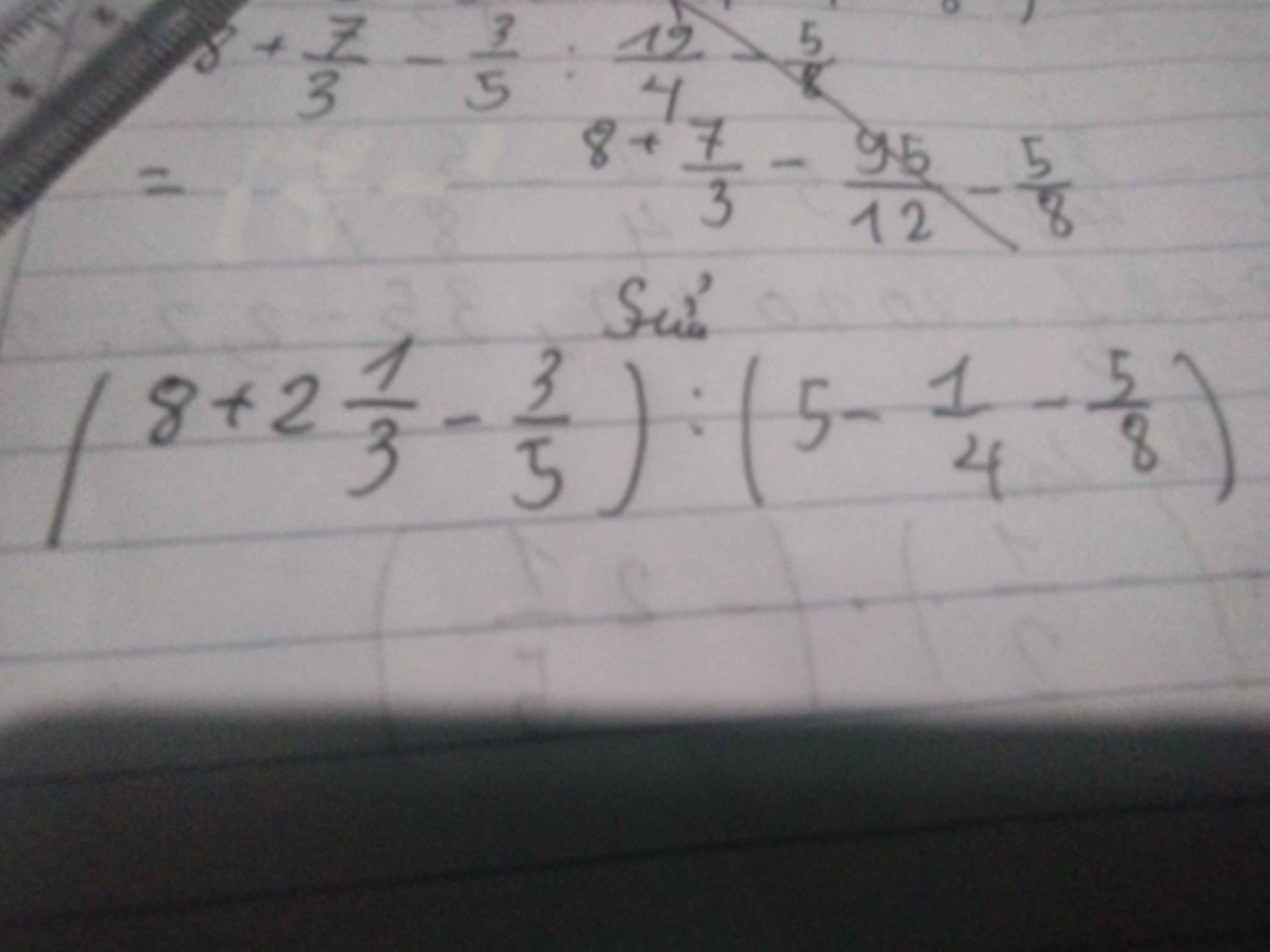
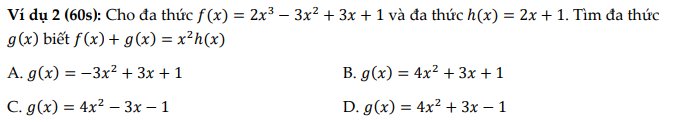


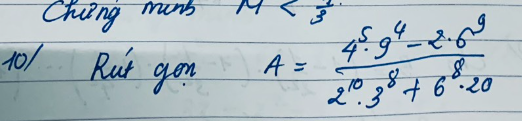


a) Ta có:
\(\left\{{}\begin{matrix}AB\perp AC\\KH\perp AC\end{matrix}\right.=>AB//KH\)
b) Ta có:
\(\widehat{ABK}=\widehat{BKI}\left(=60^o\right)\)
Mà hai góc này ở vị trí so le trong
=> AB//KI
c) AB//HK = > \(\widehat{ABK}+\widehat{HKB}=180^o\)
Mà: \(\widehat{ABK}=\widehat{BKI}\)
\(=>\widehat{BKI}+\widehat{HKB}=180^o\)
=> \(\widehat{HKI}\) là góc bẹt hay H, K, I thẳng hàng