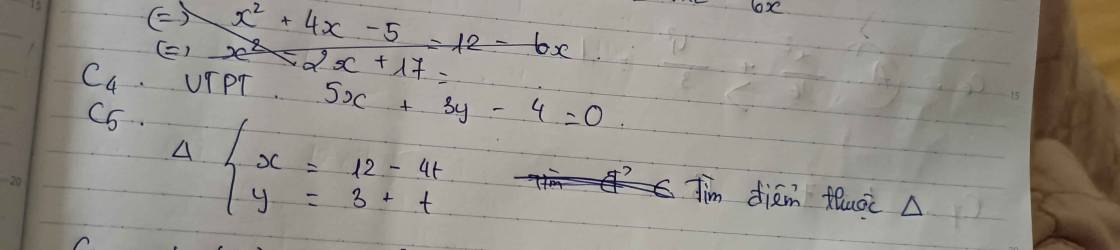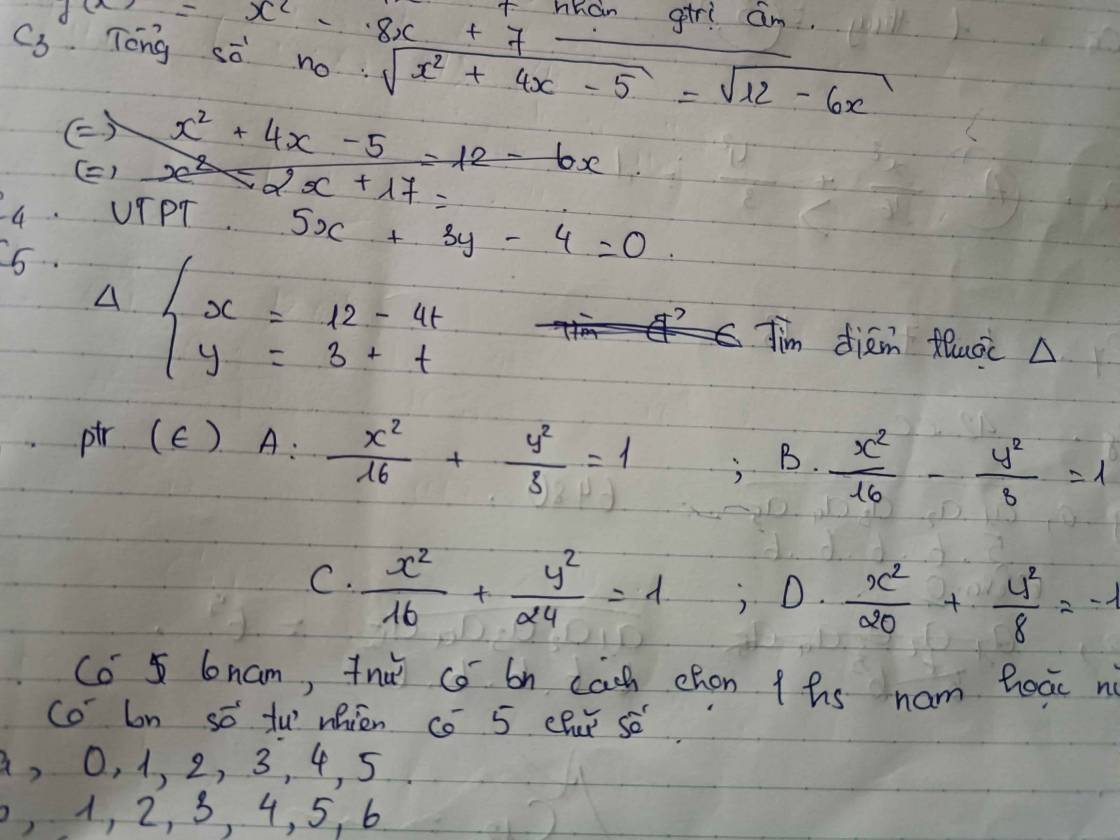Câu 5:

\(\left\{{}\begin{matrix}x=12-4t\\y=3+t\end{matrix}\right.\)(Δ)

=>\(A\left(12-4t;3+t\right)\left(t\in R\right)\) là những điểm thuộc Δ

Có \(\left|\Omega\right|=C^4_{25}\)

Gọi A là biến cố: "Có ít nhất 1 viên bi màu đỏ."

Xét biến cố \(\overline{A}:\) "Không có viên bi màu đỏ nào."

Khi đó \(\left|\overline{A}\right|=C^4_{15}\) \(\Rightarrow P\left(\overline{A}\right)=\dfrac{C^4_{15}}{C^4_{25}}=\dfrac{273}{2530}\)

\(\Rightarrow P\left(A\right)=1-P\left(\overline{A}\right)=1-\dfrac{273}{2530}=\dfrac{2257}{2530}\)

cái này mà toán lớp 10 tôi cũng lạy

Gọi các số thỏa mãn ycbt là \(\overline{\alpha\beta\gamma\delta}\)

Khi đó \(\delta\in\left\{4,6,8\right\}\) -> Có 3 cách.

TH1: \(\alpha,\beta,\gamma\) đều lẻ \(\Rightarrow\) Có \(A^3_4=24\) cách.

TH2: Trong các số \(\alpha,\beta,\gamma\) có đúng 1 số chẵn 

 \(\Rightarrow\) Có \(3.2.4.3=72\) cách.

TH3: Trong các số \(\alpha,\beta,\gamma\) có đúng 1 số lẻ.

 \(\Rightarrow\) Có \(3.4.2.1=24\) cách.

 \(\Rightarrow\) Có tất cả \(24+72+24=120\) cách chọn bộ \(\left(\alpha,\beta,\gamma\right)\)

 \(\Rightarrow\) Có tất cả \(3.120=360\) số thỏa mãn ycbt.

bạn thử đếm đi