cửa hàng đã bán 10 thùng dầu ăn , mỗi thùng chứa 6 chai dầu.hỏi cửa hàng đã bán tất cả bao nhiêu chai dầu?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Chọn hệ trục tọa độ Mxyz (M là gốc tọa độ) sao cho Mx trùng với tia MB, My trùng với tia MA và Mz cùng phương với BB' sao cho \(\overrightarrow{BB'}\) hướng theo chiều dương của Mz.
Gọi chiều cao lăng trụ là \(h>0\)
Khi đó \(B\left(a;0;0\right)\), \(C'\left(-a;0;h\right)\), \(A'\left(0;a\sqrt{3};h\right)\)
Ta có \(\overrightarrow{MC'}=\left(-a;0;h\right),\overrightarrow{BA'}=\left(-a;a\sqrt{3};h\right)\)
\(\Rightarrow\left[\overrightarrow{MC'},\overrightarrow{BA'}\right]=\left(-ah\sqrt{3};0;a^2\sqrt{3}\right)\)
\(\Rightarrow\left|\left[\overrightarrow{MC'},\overrightarrow{BA'}\right]\right|=\sqrt{\left(-ah\sqrt{3}\right)^2+\left(a^2\sqrt{3}\right)^2}=a\sqrt{3h^2+3a^2}\)
Lại có \(\overrightarrow{MB}=\left(a;0;0\right)\)
\(\Rightarrow\left[\overrightarrow{MC'},\overrightarrow{BA'}\right].\overrightarrow{MB}=-a^2h\sqrt{3}\)
\(\Rightarrow d\left(MC',BA'\right)=\dfrac{\left|\left[\overrightarrow{MC'},\overrightarrow{BA'}\right].\overrightarrow{MB}\right|}{\left|\left[\overrightarrow{MC'},\overrightarrow{BA'}\right]\right|}\) \(=\dfrac{a^2h\sqrt{3}}{a\sqrt{3a^2+3h^2}}=\dfrac{ah}{\sqrt{a^2+h^2}}\)
Theo đề bài, ta có: \(\dfrac{ah}{\sqrt{a^2+h^2}}=\dfrac{a}{2}\)
\(\Leftrightarrow\dfrac{h}{\sqrt{a^2+h^2}}=\dfrac{1}{2}\)
\(\Leftrightarrow2h=\sqrt{a^2+h^2}\)
\(\Leftrightarrow4h^2=a^2+h^2\)
\(\Leftrightarrow3h^2=a^2\)
\(\Leftrightarrow h=\dfrac{a}{\sqrt{3}}\)
\(\Rightarrow V=S_đ.h=\dfrac{\left(2a\right)^2\sqrt{3}}{4}.\dfrac{a}{\sqrt{3}}=a^3\)
Vậy thể tích lăng trụ bằng \(a^3\)

a)
\(\dfrac{x^4+12x^2-5x}{-x}=-\dfrac{x^4}{x}-\dfrac{12x^2}{x}+\dfrac{-5x}{-x}=-x^3-12x+5\)
b)
\(\dfrac{15x^5y^9-10x^3y^5+25x^4y^4}{5x^2y^2}=\dfrac{15x^5y^9}{5x^2y^2}-\dfrac{10x^3y^5}{5x^2y^2}+\dfrac{25x^4y^4}{5x^2y^2}=3x^3y^7-2xy^3+5x^2y^2\)
`a)`
`(x^4 + 12x^2 -5x):(-x)`
`=[x^4 : (-x)] + [12x^2 : (-x)] - [5x:(-x)]`
`=-x^3 - 12x + 5`
`b)`
`(15 x^5 y^9 - 10 x^3 y^5 + 25 x^4 y^4) : 5x^2 y^2`
`=(15 x^5 y^9 : 5 x^2 y^2) - (10 x^3 y^5 : 5x^2 y^2) + (25 x^4 y^4 : 5 x^2 y^2)`
`=3 x^3 y^7 - 2 x y^3 + 5 x^2 y^2`

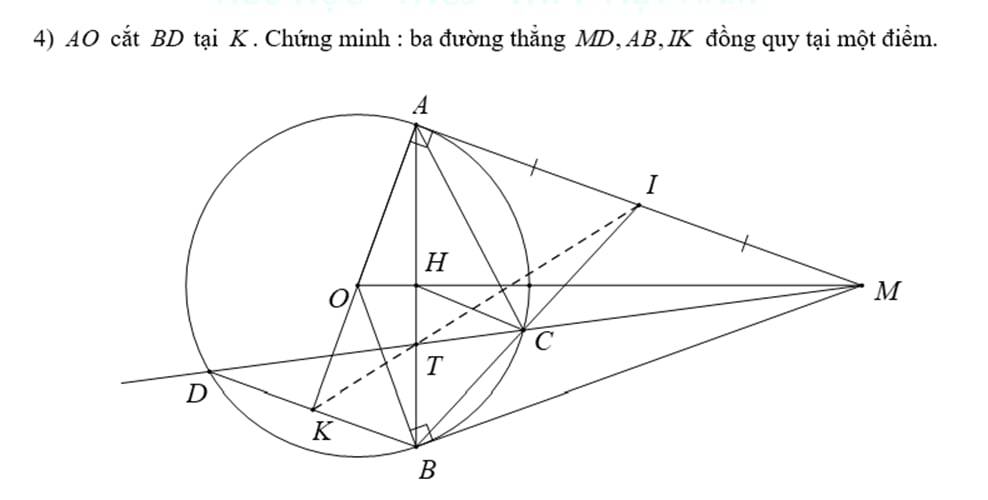
4)
Ta có:
AM // BD (cmt)
AO ⊥ AM (do MA là tiếp tuyến của (O) tại A)
⇒ AO ⊥ BD tại K
⇒ K là trung điểm của BD
Áp dụng định lý Thales đảo vào ∆AMT và ∆TBD, ta có:
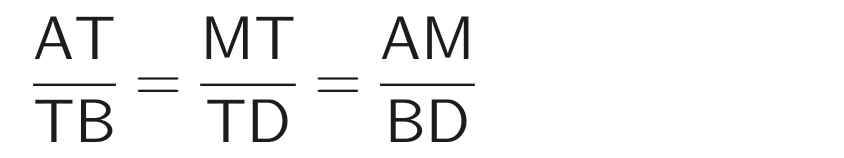
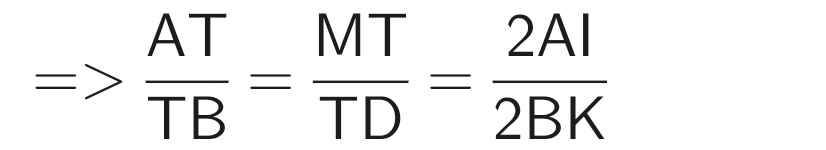
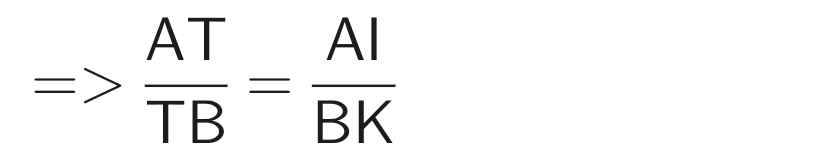 Xét ∆ATI và ∆BTK có:
Xét ∆ATI và ∆BTK có:
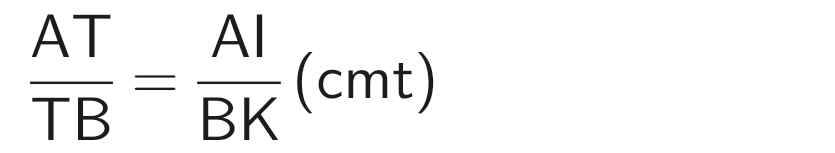 ∠IAT = ∠KBT (so le trong)
∠IAT = ∠KBT (so le trong)
⇒ ∆ATI ∽ ∆BTK (c-g-c)
⇒ ∠ATI = ∠BTK
⇒ ∠ATI và ∠BTK đối đỉnh
⇒ I, T, K thẳng hàng
⇒ T ∈ IK
⇒ MD, AB, IK đồng quy tại T

a + b = m
a - b = n
=> a = (m + n)/2
b = (m - n)/2
Có: a.b = (m + n)/2.(m - n)/2
= (m^2 - n^2)/4
=> a^3 - b^3 = (m + n)^3/2^3 - (m - n)^2/2^3
= (m + n)^3/8 - (m - n)^3/8
= [(m + n)^3 - (m - n)^3]/8
= [(m + n - m + n)((m + n)^2 + (m + n)(m - n) + (m - n)^2)]/8
= [n(m^2 + n^2 + 2mn + m^2 - n^2 + m^2 + n^2 - 2mn)]/8
= n(3m^2 + 2n^2)/8
= m^2n − (m^2−n^2)/4 .n

Gọi H,K lần lượt là trung điểm của AD,BC
Xét hình thang ABCD có
H,K lần lượt là trung điểm của AD,BC
=>HK là đường trung bình của hình thang ABCD
=>HK//AB//CD và \(HK=\dfrac{AB+CD}{2}=17\left(cm\right)\)
Xét ΔDAB có
H,M lần lượt là trung điểm của DA,DB
=>HM là đường trung bình của ΔDAB
=>HM//AB và \(HM=\dfrac{AB}{2}=\dfrac{15}{2}=7,5\left(cm\right)\)
Xét ΔCAB có
N,K lần lượt là trung điểm của CA,CB
=>NK là đường trung bình của ΔCAB
=>NK//AB và \(NK=\dfrac{AB}{2}=7,5\left(cm\right)\)
Ta có: NK//AB
HK//AB
mà HK,NK có điểm chung là K
nên H,N,K thẳng hàng
Ta có: HM//AB
HK//AB
=>H,M,K thẳng hàng
=>H,M,N,K thẳng hàng
Ta có: HM+MN+NK=HK
=>MN+7,5+7,5=17
=>MN=2(cm)

Ta có:
\(92^3\equiv2\left(mod6\right)\)
\(\Rightarrow92^{30}\equiv\left(92^3\right)^{10}\left(mod6\right)\equiv2^{10}\left(mod6\right)\equiv4\left(mod6\right)\)
\(\Rightarrow92^{90}\equiv\left(92^{30}\right)^3\left(mod6\right)\equiv4^3\left(mod6\right)\equiv4\left(mod6\right)\)
\(\Rightarrow92^{93}\equiv92^{90}.92^3\left(mod6\right)\equiv4.2\left(mod6\right)\equiv2\left(mod6\right)\)
\(139^2\equiv1\left(mod6\right)\)
\(\Rightarrow139^{20}\equiv\left(139^2\right)^{10}\left(mod6\right)\equiv1^{10}\left(mod6\right)\equiv1\left(mod6\right)\)
\(\Rightarrow92^{93}+139^{20}+3\equiv2+1+3\left(mod6\right)\equiv6\left(mod6\right)\equiv0\left(mod6\right)\)
Vậy \(\left(92^{93}+139^{20}+3\right)⋮6\)

Tk:
Số vô tỉ là số viết được dưới dạng số thập phân vô hạn không tuần hoàn.
\(#SGK\)
tk
Trong toán học, các số vô tỉ là tất cả các số thực không phải là số hữu tỉ, mà là các số được xây dựng từ các tỷ số (hoặc phân số) của các số nguyên.

Gọi số sách ở ngăn thứ nhất lúc đầu là x (cuốn sách; \(x\in\mathbb{N}^*\))
Số sách ở ngăn thứ hai lúc đầu là: \(400-x\) (cuốn sách)
Số sách ở ngăn thứ nhất nếu chuyển đi 80 cuốn sách là: \(x-80\) (cuốn sách)
Số sách ở ngăn thứ hai nếu thêm 80 cuốn sách là: \(400-x+80=480-x\) (cuốn sách)
Vì sau khi chuyển sách, số sách ở ngăn thứ hai gấp 3 lần số sách ở ngăn thứ nhất nên ta có phương trình:
\(480-x=3\left(x-80\right)\)
\(\Leftrightarrow480-x=3x-240\)
\(\Leftrightarrow4x=720\)
\(\Leftrightarrow x=180\left(tm\right)\)
Khi đó, số sách ở ngăn thứ hai lúc đầu là: \(400-180=220\) (cuốn sách)
Vậy: ...


Cửa hàng đã bán tất cả số chai dầu là:
10 x 6 = 60 (chai)
ĐS: 60 chai
Bài giải
Cửa hàng đó bán được số chai dầu là :
10 x 6 = 60 (chai)
Đáp số : 60 chai dầu .