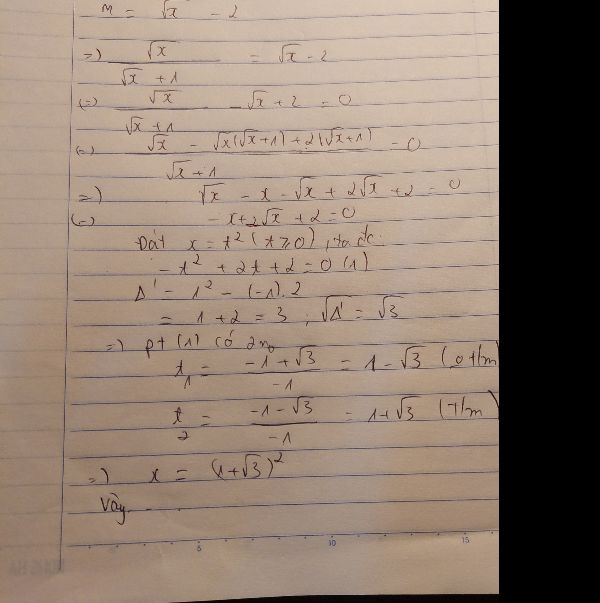Hai ngư dân đứng ở một bên bờ sông cách nhau 250m cùng nhìn thấy một cù lao trên sông với các góc nâng lần lượt là 30 độ và 40 độ. Tính khoảng cách d từ bờ sông đến cù lao
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NH
0
PN
0
VT
3
10 tháng 10 2021
\(M=\frac{\sqrt{x}}{\sqrt{x}+1}\left(x\ge0\right)\)
Khi \(M=\sqrt{x}-2\)
\(\Rightarrow\frac{\sqrt{x}}{\sqrt{x}+1}=\sqrt{x}-2\)
\(\Leftrightarrow\sqrt{x}=\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)\)
\(\Leftrightarrow\sqrt{x}=x+\sqrt{x}-2\sqrt{x}-2\)
\(\Leftrightarrow\sqrt{x}=x-\sqrt{x}-2\)
\(\Leftrightarrow x-\sqrt{x}-\sqrt{x}-2=0\)
\(\Leftrightarrow x-2\sqrt{x}+1-3=0\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)^2=3\)
\(\Leftrightarrow\left(\sqrt{x}-1\right)^2=\left(\pm\sqrt{3}\right)^2\)
\(\Leftrightarrow\sqrt{x}-1=\pm\sqrt{3}\)
\(\Leftrightarrow\sqrt{x}=\pm\sqrt{3}+1\)
\(\Leftrightarrow\orbr{\begin{cases}x=\left(\sqrt{3}+1\right)^2\\x=\left(-\sqrt{3}+1\right)^2\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=3+2\sqrt{3}+1\\1-2\sqrt{3}+3\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}x=4+2\sqrt{3}\\x=4-2\sqrt{3}\end{cases}}\)
Vậy \(x\in\left\{4\pm2\sqrt{3}\right\}\)khi \(M=\sqrt{x}-2\)
