a: Để A là số nguyên thì \(n-5⋮n+1\)

=>\(n+1-6⋮n+1\)

=>\(-6⋮n+1\)

=>\(n+1\in\left\{1;-1;2;-2;3;-3;6;-6\right\}\)

=>\(n\in\left\{0;-2;1;-3;2;-4;5;-7\right\}\)

Khi n=0 thì \(A=\dfrac{0-5}{0+1}=-5< 0\)(nhận)

Khi n=-2 thì \(A=\dfrac{-2-5}{-2+1}=\dfrac{-7}{-1}=7>0\left(loại\right)\)

Khi n=1 thì \(A=\dfrac{1-5}{1+1}=\dfrac{-4}{2}=-2< 0\)(nhận)

Khi n=-3 thì \(A=\dfrac{-3-5}{-3+1}=\dfrac{-8}{-2}=4>0\)(loại)

Khi n=2 thì \(A=\dfrac{2-5}{2+1}=\dfrac{-3}{3}=-1< 0\)(nhận)

Khi n=-4 thì \(A=\dfrac{-4-5}{-4+1}=\dfrac{-9}{-3}=3>0\left(loại\right)\)

Khi n=5 thì \(A=\dfrac{5-5}{5+1}=0\left(loại\right)\)

Khi n=-7 thì \(A=\dfrac{-7-5}{-7+1}=\dfrac{-12}{-6}=2>0\left(loại\right)\)

b: \(A=\dfrac{n-5}{n+1}=\dfrac{n+1-6}{n+1}=1-\dfrac{6}{n+1}\)

Để A có giá trị nhỏ nhất thì \(-\dfrac{6}{n+1}\) nhỏ nhất

=>\(\dfrac{6}{n+1}\) lớn nhất

=>n+1=1

=>n=0

Để A có giá trị lớn nhất thì \(\dfrac{6}{n+1}\) nhỏ nhất

=>n+1=-1

=>n=-2

\(\dfrac{64\text{x}50+44+100}{27\text{x}38+146\text{x}19}\)

\(=\dfrac{3200+144}{19\text{x}\left(27\text{x}2+146\right)}=\dfrac{3344}{19\text{x}200}\)

\(=\dfrac{3344}{3800}=\dfrac{22}{25}\)

\(\left(1-\dfrac{1}{2}\right)\times\left(1-\dfrac{1}{3}\right)\times\left(1-\dfrac{1}{4}\right)\times...\times\left(1-\dfrac{1}{2006}\right)\times\left(1-\dfrac{1}{2007}\right)\\ =\dfrac{1}{2}\times\dfrac{2}{3}\times\dfrac{3}{4}\times...\times\dfrac{2005}{2006}\times\dfrac{2006}{2007}\\ =\dfrac{1}{2007}\)

Tập xác định \(D=ℝ\backslash\left\{2\right\}\)

TCĐ: \(x=2\)

Có \(\dfrac{x^2-x-1}{x-2}=\dfrac{x^2-x-2+1}{x-2}=\dfrac{\left(x+1\right)\left(x-2\right)+1}{x-2}=\left(x+1\right)+\dfrac{1}{x-2}\)

nên đồ thị hàm số có tiệm cận xiên là đường \(y=x+1\)

Có \(y'=\dfrac{x^2-4x+3}{\left(x-2\right)^2}\)

\(y'=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=3\end{matrix}\right.\)

BBT

a: Số báo còn lại trong thư viện chiếm:

\(1-\dfrac{3}{5}=\dfrac{2}{5}\)(tổng số báo)

Số truyện còn lại trong thư viện chiếm:

\(1-\dfrac{2}{7}=\dfrac{5}{7}\)(tổng số truyện)

b: Số truyện còn lại là:

\(30:\left(1,5-1\right)\times1,5=30:0,5\times1,5=90\left(quyển\right)\)

Số báo còn lại là:

90:1,5=60(quyển)

Số truyện ban đầu là \(90:\dfrac{5}{7}=90\times\dfrac{7}{5}=126\left(quyển\right)\)

Số báo ban đầu là \(60:\dfrac{2}{5}=150\left(quyển\right)\)

Tổng số báo và truyện là:

150+126=276(quyển)

1h15p=1,25(giờ)

Vận tốc lúc xuôi dòng là:

22,6+2,2=24,8(km/h)

Độ dài quãng sông AB là:

24,8x1,25=31(km)

136 nghìn đồng =100 000đ+30 000đ+6 000đ nên 

số tiền 100 000đ cần trả là:100 000:100 000=1(tờ)

số tiền 10 000đ cần trả là:30 000:10 000=3(tờ)

số tiền 1 000đ cần trả là:6 000:1 000=6(tờ)

Vậy cần trả 1 tờ 100 000đ,3 tờ 10 000đ,6 tờ 1 000đ

TICK CHO MIK VỚI NHÉ

Tú trả bác bán hàng như sau:

+ 1 tờ 100.000 đồng

+ 3 tờ 10.000 đồng

+ 6 tờ 1.000 đồng

Tổng: 1 x 100.000 + 3 x 10.000 + 6 x 1.000 = 136.000

Thỏa mãn đề bài 136.000 và mỗi loại không quá 9 tờ

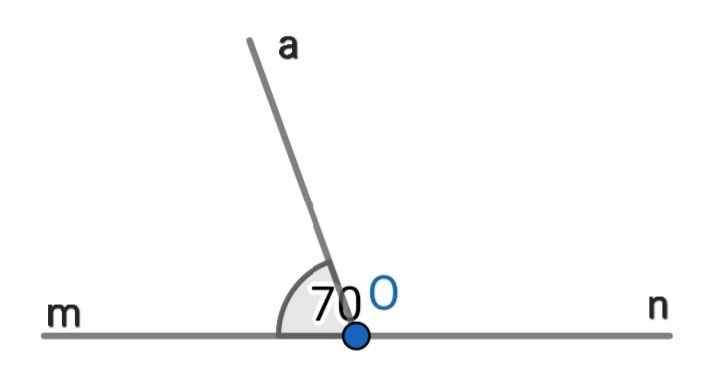  mOn là góc bẹt nên mOn = 180⁰

Thầy nghĩ là em ghi sai đề cả 2 câu a và b.

Em xem lại đề nhé!

a) \(y=\dfrac{x+1}{x-2}\)

\(y'=-\dfrac{3}{\left(x-2\right)^2}< 0\forall x\inℝ\ \left\{2\right\}\)

=> hàm số nghịch biến trên \(\left(-\infty;2\right)\) và \(\left(2;+\infty\right)\)

b) \(y=\dfrac{2x+1}{x-1}\)

\(y'=-\dfrac{3}{\left(x-1\right)^2}< 0\forall x\inℝ\ \left\{1\right\}\)

=> hàm số nghịch biến trên \(\left(-\infty;1\right)\) và \((1;+\infty)\)

TA CÓ:a:5 dư 3 suy ra:a+2 chia hết cho 5

                          suy ra a+17 chia hết cho 5    (1)

           a:7 dư 4 suy ra a+3 chia hết cho 7

                         suy ra a+17 chia hết cho 7      (2)

Từ (1) và (2) suy ra a+17 thuộc BC của 7 và 5

mà a nhỏ nhất nên a+17 thuộc BCNN của 7 và 5=35

suy ra a=35-17=18

Vậy a=18

TICK CHO MIK VỚI NHÉ

18