Giúp mình với ạ
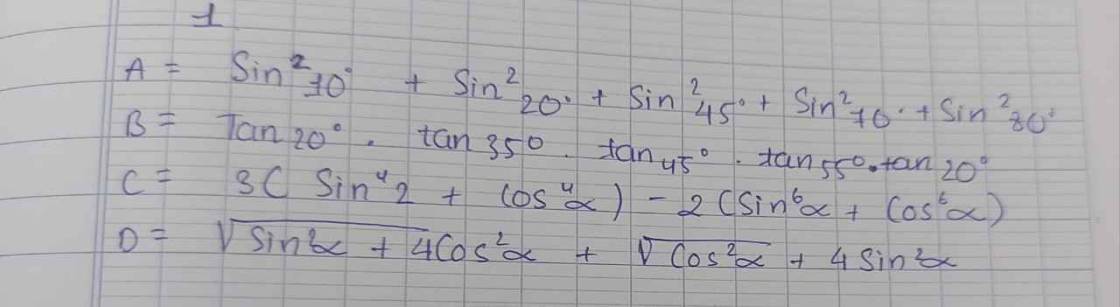
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(cos\left(x-15^0\right)=\dfrac{\sqrt{2}}{2}\)
=>\(\left[{}\begin{matrix}x-15^0=45^0+k\cdot360^0\\x-15^0=-45^0+k\cdot360^0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=60^0+k\cdot360^0\\x=-30^0+k\cdot360^0\end{matrix}\right.\)
b: \(cos\left(2x+\dfrac{\Omega}{3}\right)+cos\left(x-\dfrac{\Omega}{3}\right)=0\)
=>\(cos\left(2x+\dfrac{\Omega}{3}\right)=-cos\left(x-\dfrac{\Omega}{3}\right)\)
=>\(cos\left(2x+\dfrac{\Omega}{3}\right)=cos\left(\Omega-x+\dfrac{\Omega}{3}\right)\)
=>\(cos\left(2x+\dfrac{\Omega}{3}\right)=cos\left(-x+\dfrac{4\Omega}{3}\right)\)
=>\(\left[{}\begin{matrix}2x+\dfrac{\Omega}{3}=-x+\dfrac{4\Omega}{3}+k2\Omega\\2x+\dfrac{\Omega}{3}=x-\dfrac{4}{3}\Omega+k2\Omega\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=\Omega+k2\Omega\\x=-\dfrac{5}{3}\Omega+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=\dfrac{\Omega}{3}+\dfrac{k2\Omega}{3}\\x=-\dfrac{5}{3}\Omega+k2\Omega\end{matrix}\right.\)
c: \(sin\left(3x+1\right)=sin\left(x-2\right)\)
=>\(\left[{}\begin{matrix}3x+1=x-2+k2\Omega\\3x+1=\Omega-x+2+k2\Omega\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=-3+k2\Omega\\4x=1+\Omega+k2\Omega\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=-\dfrac{3}{2}+k\Omega\\x=\dfrac{1}{4}+\dfrac{\Omega}{4}+\dfrac{k\Omega}{2}\end{matrix}\right.\)

Bài 3:
1/2 của 16 là \(16\times\dfrac{1}{2}=\dfrac{16}{2}=8\)
1/5 của 20 là \(20\times\dfrac{1}{5}=\dfrac{20}{5}=4\)
Bài 2: Hình tròn này có 4 phần
Bài 1:
55+7=62
45+7=52
56+9=65
Bài 4:
Nếu năm 2024 bạn đang học lớp 4 thì có nghĩa là bạn 9 tuổi
=>Năm sinh của bạn là 2024-9=2015
=>Năm 2009 thì vào thời điểm đó, bạn chưa ra đời

\(24:6+36:6\)
\(=\left(24+36\right):6\)
\(=60:6\)
\(=10\)

Số x là :
\(13614\times424+422=5772758\)
Đáp số : \(x=5772758\)

Số vải bán được trong ngày thứ ba gấp ngày thứ hai số lần là :
\(1:\dfrac{2}{3}=\dfrac{3}{2}\) ( lần )
\(10\) mét vải gấp số vải bán được trong ngày thứ hai số lần là :
\(2-\dfrac{3}{2}=\dfrac{1}{2}\) ( lần )
Số mét vải bán được trong ngày thứ hai là :
\(10:\dfrac{1}{2}=20\) ( mét )
Số mét vải bán được trong ngày thứ nhất là :
\(20\times2=40\) ( mét )
Số mét vải bán được trong ngày thứ ba là :
\(40-10=30\) ( mét )
Đáp số :
ngày thứ nhất : \(40\) mét
ngày thứ hai : \(20\) mét
ngày thứ ba : \(30\) mét


Bài 4:
a: Đặt 2x+10=0
=>2x=-10
=>x=-5
b: Đặt 4(x-1)+3x-5=0
=>4x-4+3x-5=0
=>7x=9
=>\(x=\dfrac{9}{7}\)
c: Đặt \(-1\dfrac{1}{3}x^2+x=0\)
=>\(\dfrac{4}{3}x^2-x=0\)
=>\(x\left(\dfrac{4}{3}x-1\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\\dfrac{4}{3}x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{3}{4}\end{matrix}\right.\)
Bài 5:
a: Xét ΔBAD vuông tại A và ΔBMD vuông tại M có
BD chung
\(\widehat{ABD}=\widehat{MBD}\)
Do đó: ΔBAD=ΔBMD
b: ΔBAD=ΔBMD
=>BA=BM và DA=DM
ta có: BA=BM
=>B nằm trên đường trung trực của AM(1)
Ta có: DA=DM
=>D nằm trên đường trung trực của AM(2)
Từ (1),(2) suy ra BD là đường trung trực của AM
c: Xét ΔBKC có
KM,CA là các đường cao
KM cắt CA tại D
Do đó: D là trực tâm của ΔBKC
=>BD\(\perp\)KC tại N

Vì \(37254\) chia x được \(146\) ( dư \(170\) ) nên :
\(37254-170=37084\) là số chia x được \(146\)
Số x là :
\(37084:146=254\)
Đáp số : \(x=254\)

Gọi T là giao điểm của 2 tiếp tuyến tại A và B của (O). Qua N kẻ đường thẳng song song với AM cắt AB tại C. Gọi I là giao điểm của AB và MN.
Khi đó, theo tính chất của 2 tiếp tuyến cắt nhau, ta có \(TA=TB\) \(\Rightarrow\Delta TAB\) cân tại T \(\Rightarrow\widehat{TBA}=\widehat{TAB}\)
Vì NC//TA nên \(\widehat{NCB}=\widehat{TAB}\) (2 góc đồng vị)
Từ đó \(\Rightarrow\widehat{TBA}=\widehat{NCB}\) \(\Rightarrow\Delta NCB\) cân tại N
\(\Rightarrow NC=NB\)
Mà \(NB=MA\) nên \(NC=MA\)
Do đó tứ giác NAMC là hình bình hành (vì có NC//MA và \(NC=MA\))
\(\Rightarrow\) MN và AC cắt nhau tại trung điểm I của mỗi đoạn
\(\Rightarrow\) I là trung điểm MN
\(\Rightarrow\) AB chia đôi MN (đpcm)
\(A=sin^210^0+sin^220^0+sin^245^0+sin^270^0+sin^280^0\)
\(=\left(sin^210^0+sin^280^0\right)+\left(sin^220^0+sin^270^0\right)+sin^245^0\)
\(=\left(sin^210^0+cos^210^0\right)+\left(sin^220^0+cos^220^0\right)+\dfrac{1}{2}\)
\(=1+1+\dfrac{1}{2}=\dfrac{5}{2}\)
\(B=tan20^0\cdot tan35^0\cdot tan45^0\cdot tan55^0\cdot tan20^0\)
\(=tan^220^0\cdot tan35^0\cdot cot35^0\cdot1=tan^220^0\)
\(C=3\cdot\left(sin^4\alpha+cos^4\alpha\right)-2\left(sin^6\alpha+cos^6\alpha\right)\)
\(=3\left[\left(sin^2\alpha+cos^2\alpha\right)^2-2\cdot sin^2\alpha\cdot cos^2\alpha\right]-2\left[\left(sin^2\alpha+cos^2\alpha\right)^3-3\cdot sin^2\alpha\cdot cos^2\alpha\cdot\left(sin^2\alpha+cos^2\alpha\right)\right]\)
\(=3\left[1-2\cdot sin^2\alpha\cdot cos^2\alpha\right]-2\left[1-3\cdot sin^2\alpha\cdot cos^2\alpha\right]\)
\(=3-6\cdot sin^2\alpha\cdot cos^2\alpha-2+6\cdot sin^2\alpha\cdot cos^2\alpha\)
=1
\(D=\sqrt{sin^2\alpha}+4\cdot cos^2\alpha+\sqrt{cos^2\alpha}+4\cdot sin^2\alpha\)
\(=\left|sin\alpha\right|+\left|cos\alpha\right|+4\cdot\left(cos^2\alpha+sin^2\alpha\right)=\left|sin\alpha\right|+\left|cos\alpha\right|+4\)