Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) 1 giờ 15 phút + 2 giờ 24 phút + 3 giờ 36 phút
= 1 giờ 15 phút + (2 giờ 24 phút + 3 giờ 36 phút)
= 1 giờ 15 phút + 6 giờ
= 7 giờ 15 phút
b) 2 giờ + 3 giờ + 1 giờ + 4 giờ
= 10 giờ
c) 10 giờ - 5 giờ 25 phút - 2 giờ 35 phút
= 10 giờ - (5 giờ 25 phút + 2 giờ 35 phút)
= 10 giờ - 8 giờ
= 2 giờ

Người đó đến thành phố lúc:
6h30p+1h20p+35p+1h15p
=7h50p+1h50p
=8h100p
=9h40p

a) Chiều cao của bể là:
\(2,4:\dfrac{6}{5}=2\left(m\right)\)
Thể tích của bể là:
\(4,5\times2,4\times2=21,6\left(m^3\right)\)
Bể chứa được tối đa số lít nước là:
\(21,6\left(m^3\right)=21600\left(dm^3\right)=21600\left(l\right)\)
b) Thể tích nước có trong bể hiện tại là:
\(4,5\times2,4\times0,6=6,48\left(m^3\right)\)
Cần đổ thêm số mét khối nước nữa cho bể đầy là:
\(21,6-6,48=15,12\left(m^3\right)\)
ĐS: ...


Ta có: AM+MC=AC
=>MC+4=24
=>MC=20(cm)
Xét ΔCAB có MN//AB
nên \(\dfrac{MN}{AB}=\dfrac{CM}{CA}\)
=>\(\dfrac{MN}{16}=\dfrac{20}{24}=\dfrac{5}{6}\)
=>\(MN=16\cdot\dfrac{5}{6}=\dfrac{40}{3}\left(cm\right)\)
ΔCMN vuông tại M
=>\(S_{CMN}=\dfrac{1}{2}\cdot CM\cdot MN=\dfrac{1}{2}\cdot20\cdot\dfrac{40}{3}=\dfrac{400}{3}\left(cm^2\right)\)
ΔAMB vuông tại A
=>\(S_{AMB}=\dfrac{1}{2}\cdot AM\cdot AB=\dfrac{1}{2}\cdot4\cdot16=32\left(cm^2\right)\)
Ta có: ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot16\cdot24=8\cdot24=192\left(cm^2\right)\)
Ta có: \(S_{AMB}+S_{MNB}+S_{CMN}=S_{CAB}\)
=>\(S_{MNB}+\dfrac{400}{3}+32=192\)
=>\(S_{MBN}=\dfrac{80}{3}\left(cm^2\right)\)
.png)

bài giải
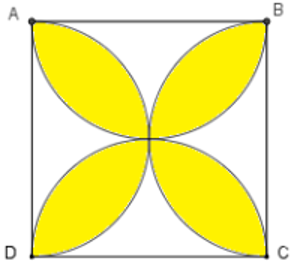
diện tích ABCD là:
4 x 4 = 16 ( cm2 )
diện tích hai nữa hình tròn là:
( 4: 2 ) x ( 4 : 2 ) x 3,14 = 12,56 ( cm2 )
diện tích phần tô đậm là:
12,56 - ( 16 - 12,56 ) = 12,12 ( cm2 )
đáp số: 12,12 cm2.