Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi vận tốc xe thứ nhất là : x (km/giờ)
ĐK : x > 30
=> Vận tốc xe thứ hai là : x - 30 (km/giờ)
+) Quãng đường xe thứ nhất đi được là : 6x (km)
+) Quãng đường xe thứ hai đi được là : 9(x-30) (km)
Vì : Quãng đường 2 xe đi được là như nhau, nên ta có phương trình :
6x = 9(x-30)
<=> 9x - 270 = 6x
<=> 9x - 6x = 270
<=> 3x = 270
<=> x = 90 (TMDK)
Vậy vận tốc xe thứ nhất là : 90km/giờ ; vận tốc xe thứ hai là : 90 - 30 = 60 (km/giờ)

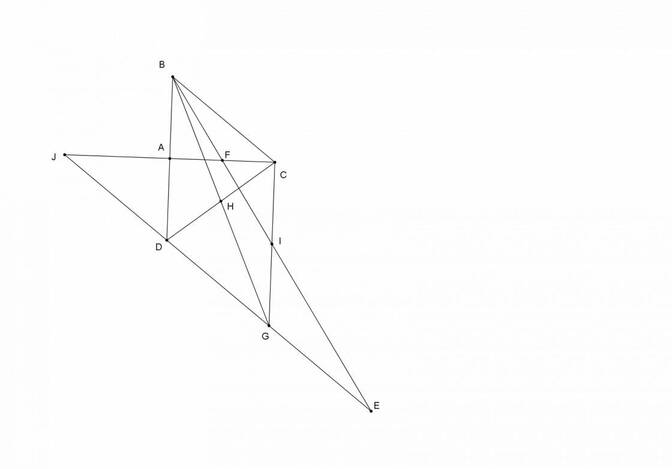
gọi $J$ là giao điểm của $DE,AC$, ta có $BCDJ $là hình thoi nên $BC\parallel JD$, $JA=AC=2CF\Rightarrow 3CF=JF$, theo Thales ta có \(\dfrac{BC}{EJ}=\dfrac{CF}{JF}=\dfrac{1}{3}\Rightarrow JE=3BC\), mà $JD=BC$ nên suy ra $DE=2BC$, hay $EG=DG=BC$, dẫn đến $BCEG,BCGD$ là hình bình hành, suy ra $H$ là trung điểm $CD,I$ là trung điểm $CG$, theo tính chất đường trung bình ta có \(IH=\dfrac{1}{2}DG=\dfrac{1}{4}DE\)

A B C D E F K
Gọi K là giao của AE và DF
Xét tg vuông BDF và tg vuông BKF có
\(\widehat{EBF}=\widehat{EKF}\) (cùng phụ với \(\widehat{BDK}\) ) (1)
=> B và K cùng nhìn EF dưới hai góc bằng nhau
=> BEFK là tứ giác nội tiếp \(\Rightarrow\widehat{EFB}=\widehat{EKB}\) (góc nt cùng chắn cung EB) (2)
Ta có \(\widehat{EBF}=\widehat{ABD}\) (gt) (3)
Từ (1) và (3) \(\Rightarrow\widehat{ABD}=\widehat{EKF}\) => B và K cùng nhìn AD dưới 2 góc bằng nhau) => ABKD là tứ giác nội tiếp
\(\Rightarrow\widehat{ADB}=\widehat{EKB}\) (góc nội tiếp cùng chắn cung AB) (4)
Xét tg ABD và tg EBF có
\(\widehat{ABD}=\widehat{EBF}\) (gt)
Từ (2) và (4) \(\Rightarrow\widehat{ADB}=\widehat{EFB}\)
\(\Rightarrow\widehat{BAC}=\widehat{BEF}\)

Áp dụng BĐT tam giác, ta có AB + BC > AC
=> 8 > AC
Áp dụng BĐT tam giác, ta có AC > AB - BC
=> AC > 6
Mà AC là số nguyên => AC = 7
Vậy...

Gọi chiều dài ban đầu là \(x\left(m\right)\) thì chiều rộng ban đầu là \(x-8\left(m\right)\)
Chiều dài sau khi thay đổi là \(x+10\left(m\right)\), chiều rộng sau khi thay đổi là \(x-8-4=x-12\left(m\right)\)
Ta có: \(x\left(x-8\right)=\left(x+10\right)\left(x-12\right)\)
\(\Rightarrow x^2-8x=x^2-12x+10x-120\)
\(\Rightarrow6x=120\Rightarrow x=20\left(m\right)\)
Vậy chiều dài ban đầu là 20m, chiều rộng ban đầu là 12m.

Gọi chiều dài của khu vườn là a (a > 0,m), khi đó chiều rộng của khu vườn là a - 8 m
Khi đó diện tích của khu vườn là a(a - 8) m2
Vì khi tăng chiều dài của khu vườn thêm 10m, giảm chiều rộng của khu vườn đi 4m thì diện tích không thay đổi.
=> Ta có a(a - 8) = (a + 10)(a - 12)
<=> a^2 - 8a = a^2 - 2a - 120
<=> 6a - 120 = 0 <=> a = 20
Vậy...

Câu 1:
a) 2x(3x+2) - 3x(2x+3) = 6x^2+4x - 6x^2-9x = -5x
b) \(\left(x+2\right)^3+\left(x-3\right)^2-x^2\left(x+5\right)\)
\(=x^3+6x^2+12x+8+x^2-6x+9-x^3-5x^2\)
\(=2x^2+6x+17\)
c) \(\left(3x^3-4x^2+6x\right)\div\left(3x\right)=x^2-\dfrac{4}{3}x+2\)

Gọi tuổi của bạn là `x`
Lấy tuổi đó cộg thêm `5`, được bao nhiêu đem nhân với `2`, lấy kq trên cộg với `10` r nhân kq vừa tìm được với `5` sau đó trừ `100` ta có biểu thức:
`[(x+5).2+10].5-100`
`=10(x+5)+50-100`
`=10x+50+50-100`
`=10x`
Ta thấy được kq của biểu thức trên bằng` 10` lần số tuổi thực của bạn, nên ta chỉ cần lấy kết quả cuối cùng chia cho `10` thì ra tuổi thực
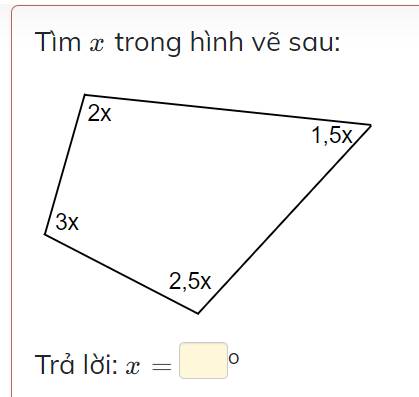
Tổng các góc trong của 1 tứ giác bằng 360 độ
\(\Rightarrow3x+2x+2,5x+1,5x=360\)
\(\Rightarrow9x=360\Rightarrow x=40^o\)