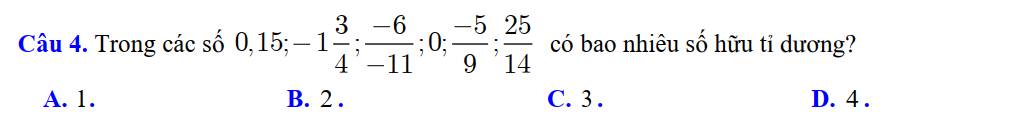Cho dãy số liên tiếp 1, 2, 3, . . . , 100. Chứng minh rằng: Nếu lấy ra 51 số bất kì sẽ luôn có 4 số a, b, c, d mà (a − b)(c − d) chia hết cho 2021.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A=\(\dfrac{1\cdot4}{2\cdot3}\) \(\cdot\dfrac{2\cdot5}{3\cdot4}\) ...\(\dfrac{2015\cdot2018}{2016\cdot2017}\)
A=\(\dfrac{1\cdot2\cdot3\cdot...\cdot2015}{1\cdot2\cdot3\cdot...\cdot2016}\) \(\cdot\dfrac{4\cdot5\cdot...\cdot2018}{3.4\cdot...\cdot2017}\)
A=\(\dfrac{1}{2016}\) \(\cdot\dfrac{2018}{3}\) =\(\dfrac{1009}{336}\)


50:làm tròn đến hàng trăm
5:làm tròn đên hàng chục
0,5:làm tròn đên hàng đơn vị
0,05:làm tròn đến phần mười,số thập phân thứ nhất
0,005:làm tròn đến phần nghìn,số thập phân thứ 2


\(a.\dfrac{-3}{8}-\dfrac{13}{65}+\dfrac{3}{8}=\left(\dfrac{3}{8}-\dfrac{3}{8}\right)-\dfrac{13}{65}=-\dfrac{13}{65}\)
\(b.\left(\dfrac{-13}{7}-\dfrac{4}{9}\right)-\left(-\dfrac{10}{7}-\dfrac{4}{9}\right)=\dfrac{-13}{7}-\dfrac{4}{9}+\dfrac{10}{7}+\dfrac{4}{9}\\ =\left(\dfrac{-13}{7}+\dfrac{10}{7}\right)+\left(\dfrac{4}{9}-\dfrac{4}{9}\right)=-\dfrac{3}{7}\)
\(c.17\dfrac{1}{3}\cdot\left(\dfrac{-3}{7}\right)+3\dfrac{2}{3}\cdot\left(\dfrac{-3}{7}\right)=\dfrac{-3}{7}\cdot\left(17\dfrac{1}{3}+3\dfrac{2}{3}\right)\\ =\dfrac{-3}{7}\cdot\left(\dfrac{52}{3}+\dfrac{11}{3}\right)=\dfrac{-3}{7}\cdot21=-9\)



Có 3 số hữu tỉ dương là \(0,15;\dfrac{-6}{-11}=\dfrac{6}{11};\dfrac{25}{14}\)
Chọn C