Rút gọn biểu thức :
a) A = /2+x/-/3x-1/
b) B =0,4*/x/-4*/x-3/
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


|x+5/3 | -1/2=3/4
|x-5/3| = 3/4 +1/2
|x-5/3|=3/4 + 2/4
|x-5/3|=5/4
=> x- 5/3=5/4 hay x-5/3=-5/4
x= 5/4+5/3 x=-5/4+5/3
=> x=35/12 x=5/12

Áp dụng t/c của dãy tỉ số bằng nhau, ta có:
\(\frac{b+c+d}{a}=\frac{a+c+d}{b}=\frac{a+b+d}{c}=\frac{a+b+c}{d}=k\)
\(=\frac{b+c+d+a+c+d+a+b+d+a+b+c}{a+b+c+d}\)
= \(\frac{3b+3c+3a+3d}{a+b+c+d}=\frac{3\left(a+b+c+d\right)}{a+b+c+d}=3\)(Do a + b + c + d \(\ne\)0)
=> k = 3
Với k = 3 => M = (3 - 3)2019 = 0

Ta có:
\(x^2+y^2=1\Rightarrow\left(x^2+y^2\right)^2=1\)(1)
Thay (1) vào \(\frac{x^4}{a}+\frac{y^4}{b}=\frac{1}{a+b}\)ta có:
\(\frac{x^4}{a}+\frac{y^4}{b}=\frac{\left(x^2+y^2\right)^2}{a+b}\Leftrightarrow\frac{x^4b+y^4a}{ab}=\frac{x^4+2x^2y^2+y^4}{a+b}\)
\(\Leftrightarrow\left(x^4b+y^4a\right)\left(a+b\right)=\left(x^4+2x^2y^2+y^4\right).ab\)
\(\Leftrightarrow x^4ab+x^4b^2+y^4a^2+y^4ab=x^4ab+2x^2y^2ab+y^4ab\)
\(\Leftrightarrow x^4b^2+y^4a^2=2x^2y^2ab\)
\(\Leftrightarrow\left(x^2b\right)^2-2x^2y^2ab+\left(y^2a\right)^2=0\)
\(\Leftrightarrow\left(x^2b-y^2a\right)^2=0\)
\(\Leftrightarrow x^2b-y^2a=0\)
\(\Leftrightarrow x^2b=y^2a\)
\(\Rightarrow\frac{x^2}{a}=\frac{y^2}{b}=\frac{x^2+y^2}{a+b}=\frac{1}{a+b}\)
\(\Rightarrow\left(\frac{x^2}{a}\right)^{1002}=\left(\frac{y^2}{b}\right)^{1002}=\left(\frac{1}{a+b}\right)^{1002}\)
\(\Rightarrow\frac{x^{2004}}{a^{1002}}=\frac{y^{2004}}{b^{1002}}=\frac{1}{\left(a+b\right)^{1002}}\)
\(\Rightarrow\frac{x^{2004}}{a^{1002}}+\frac{y^{2004}}{b^{1002}}=\frac{1}{\left(a+b\right)^{1002}}+\frac{1}{\left(a+b\right)^{1002}}=\frac{2}{\left(a+b\right)^{1002}}\left(đpcm\right)\)
Chúc bạn học tốt!

umk cái này căng vì lp 7 chưa học bất đẳng thức ( nếu hoặc học thêm có thể có)
ta có |x-2018|+|x-2019| = | x-2018|+|2019-x|
>= |x-2018+2019-x| = |1| = 1
=> GTNN của Bt = 1
dấu "=" xảy ra (=) (x-2018)(2019-x)>=0
(=) hoặc 2018<=x<=2019
Note: nếu giáo viên hỏi j thêm bn cứ nói em hỏi anh chị lớp trên ( anh chị ruột hay họ j cx đc) chứ đừng nói tự mày mò ra nha
học tốt

\(\sqrt{x-5}\)=\(\sqrt{4}\)
=> x- 5 = 4
x = 4+5
x = 9

M′M′ là ảnh của mắt MM cho bởi gương KIKI.
Trong các tia sáng đi từ tường tới gương, hai tia ngoài cùng cho tia phản xạ lọt vào mắt của KMKM và IMIM, ứng với hai tia tới PKPK và QIQI. Hai tia tới PKPK và QIQI đều có đường kéo dài đi qua M′M′.

Cách vẽ PQ: Đầu tiên vẽ ảnh M′M′ của MM (MM′⊥KIMM′⊥KI và M′H=MHM′H=MH), sau đó nối M′KM′K và kéo dài cắt tưởng ở PP và M′IM′I cắt tường ở QQ.
PQPQ là khoảng tường quan sát được trong gương.
b. Nếu người tiến lại gần gương thì ảnh M′M′ cũng tiến lại gần gương, góc KM′IKM′I to ra nên khoảng PQPQ cũng to ra hơn.
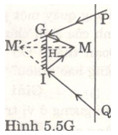
a) M’ là ảnh của mắt M cho bởi gương GI (hình 5.5G). Trong các tia sáng đi từ tường tới gương, hai tia ngoài cùng cho tia phản xạ lọt vào mắt là GM và IM, ứng với hai tia tới là PG và QI. Hai tia tới PG và QI đều có đường kéo dài đi qua M’ề Cách vẽ PQ như sau: Đầu tiên vẽ ảnh M’ của M (MM 1 GI và M’H = MH), sau đó nối M’G và kéo dài cắt tường ở p và M’I cắt tường ở Q. PQ là khoảng tường quan sát được trong gương.
b) Nếu người tiến lại gần gương thì ảnh M’ cũng tiến lại gần gương, góc GM1 to ra nên khoảng PQ cũng to ra hơn.
Học tốt !
a)A=2+x-3x+1
A=3-2x
b)0,4x-4x+12
=12-3,6x