giúp mik với mik đang cần: D=3^0+3^1+3^2+3^3+...+3^302
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


N là số cần tìm ,ta có:
[n×(n-1)]:2=1770
n×(n-1)=59×60=60×(60-1)
=>n=60
Vậy n=60

Gọi số học sinh của lớp 6A là x(bạn)
(Điều kiện: \(x\in Z^+\))
Số học sinh xuất sắc của lớp 6A là \(\dfrac{5}{9}x\left(bạn\right)\)
Số học sinh đạt của lớp 6A là \(x-\dfrac{5}{9}x-\dfrac{1}{3}x=\dfrac{1}{9}x\left(bạn\right)\)
Do đó, ta có: \(\dfrac{1}{9}x=5\)
=>x=5*9=45(nhận)
Vậy: Số học sinh xuất sắc là \(45\cdot\dfrac{5}{9}=25\left(bạn\right)\)

Gọi d=ƯCLN(2n+3;4n+4)
=>\(\left\{{}\begin{matrix}2n+3⋮d\\4n+4⋮d\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}4n+6⋮d\\4n+4⋮d\end{matrix}\right.\)
=>\(4n+6-4n-4⋮d\)
=>\(2⋮d\)
mà 2n+3 lẻ
nên d=1
=>ƯCLN(2n+3;4n+4)=1
=>\(B=\dfrac{2n+3}{4n+4}\) là phân số tối giản

Vận tốc của An là 50*1,5=75(km/h)
Thời gian An đi từ B đến chỗ gặp là:
\(6h40p-6h20p=20p=\dfrac{1}{3}\left(giờ\right)\)
Thời gian Bình đi từ A đến chỗ gặp là
6h40p-6h=40p=2/3(giờ)
Độ dài quãng đường An đi từ B đến chỗ gặp là:
\(75\cdot\dfrac{1}{3}=25\left(km\right)\)
Độ dài quãng đường Bình đi từ A đến chỗ gặp là:
\(50\cdot\dfrac{2}{3}=\dfrac{100}{3}\left(km\right)\)
Độ dài quãng đường AB là \(\dfrac{100}{3}+25=\dfrac{175}{3}\left(km\right)\)

d: \(\dfrac{-3}{-4}:\left(\dfrac{7}{-5}\cdot\dfrac{-5}{2}\right)\)
\(=\dfrac{3}{4}:\dfrac{7}{2}\)
\(=\dfrac{3}{4}\cdot\dfrac{2}{7}=\dfrac{3}{2\cdot7}=\dfrac{3}{14}\)
h: \(\dfrac{-5}{-16}\cdot\left(\dfrac{7}{44}\cdot\dfrac{32}{-5}\right)\)
\(=-\dfrac{5}{16}\cdot\dfrac{7}{44}\cdot\dfrac{32}{5}\)
\(=-\dfrac{5}{5}\cdot\dfrac{32}{16}\cdot\dfrac{7}{44}\)
\(=-2\cdot\dfrac{7}{44}=-\dfrac{7}{22}\)

\(A=1+2+2^2+...+2^{2024}\)
\(=\left(1+2+2^2\right)+\left(2^3+2^4+2^5\right)+...+\left(2^{2022}+2^{2023}+2^{2024}\right)\)
\(=\left(1+2+2^2\right)+2^3\left(1+2+2^2\right)+...+2^{2022}\left(1+2+2^2\right)\)
\(=7\cdot\left(1+2^3+...+2^{2022}\right)⋮7\)
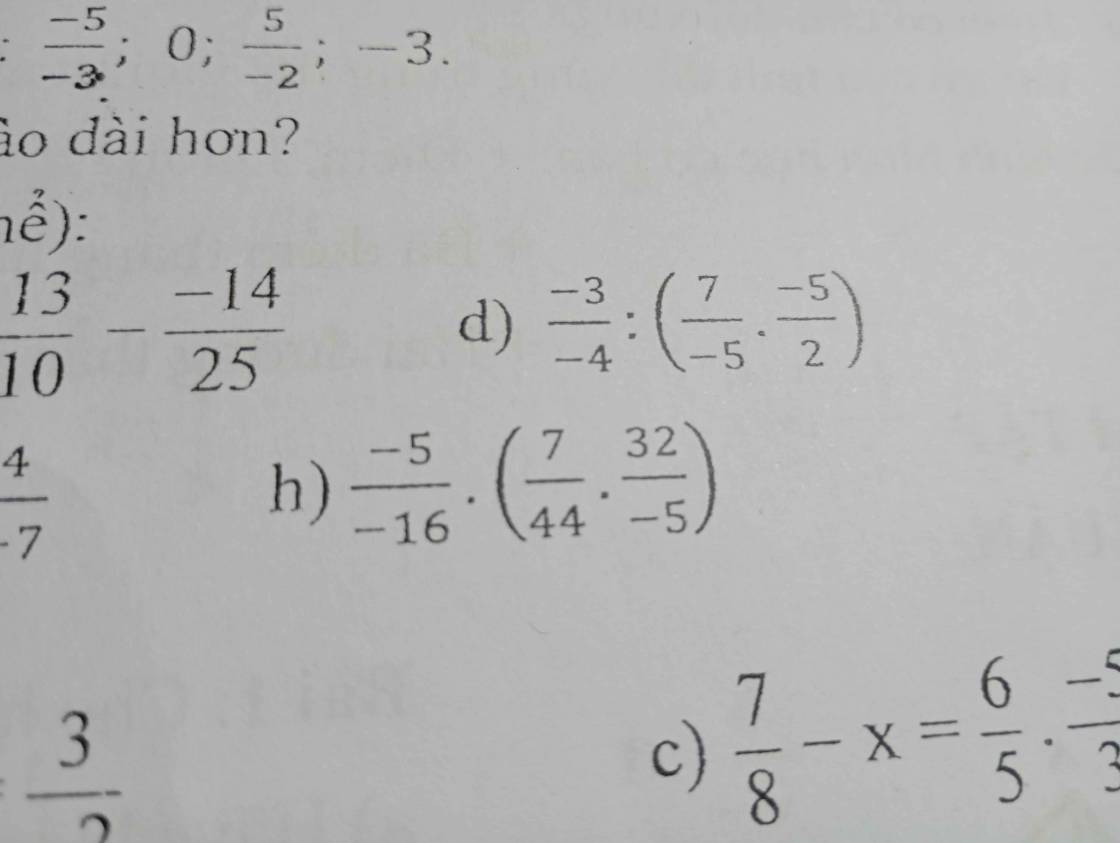
\(D=3^0+3^1+...+3^{302}\)
=>\(3\cdot D=3+3^2+...+3^{303}\)
=>\(3D-D=3+3^2+...+3^{303}-3^0-3^1-...-3^{302}\)
=>\(2D=3^{303}-1\)
=>\(D=\dfrac{3^{303}-1}{2}\)