Hai đường thẳng y = kx + (m – 2) và y = (5 – k)x + (4 – m) trùng nhau khi và chỉ khi:

    k = 5 – k (1) và m – 2 = 4 – m (2)

Từ (1) suy ra k = 2,5 (thỏa mãn điều kiện k ≠ 0 và k ≠ 5)

Từ (2) suy ra m = 3

Vậy với k = 2,5 và m = 3 thì hai đường thẳng trùng nhau.

Hai đường thẳng y = kx + (m – 2) và y = (5 – k)x + (4 – m) trùng nhau khi và chỉ khi:

    k = 5 – k (1) và m – 2 = 4 – m (2)

Từ (1) suy ra k = 2,5 (thỏa mãn điều kiện k ≠ 0 và k ≠ 5)

Từ (2) suy ra m = 3

Vậy với k = 2,5 và m = 3 thì hai đường thẳng trùng nhau.

Theo đề bài ta có b ≠ b' (vì 2 ≠ 1)

Nên hai đường thẳng y = (a – 1)x + 2 và y = (3 – a)x + 1 song song với nhau khi và chỉ khi:

    a – 1 = 3 – a

=> a = 2 (thỏa mãn a ≠ 1 và a ≠ 3)

Vậy với a = 2 thì hai đường thẳng song song với nhau.

a) Hàm số y=(a–1)x+a(a≠1)y=(a–1)x+a(a≠1) là hàm số bậc nhất có đồ thị hàm số cắt trục tung

tại điểm có tung độ bằng y = 2 nên a = 2.

b) Hàm số y=(a–1)x+a(a≠1)y=(a–1)x+a(a≠1) là hàm số bậc nhất có đồ thị hàm số cắt trục hoành tại điểm có hoành độ x = -3 nên tung độ giao điểm này bằng 0.

Ta có:

0=(a–1)(–3)+a⇔–3x+3+a=0⇔–2a=–3⇔a=1,50=(a–1)(–3)+a⇔–3x+3+a=0⇔–2a=–3⇔a=1,5                                   

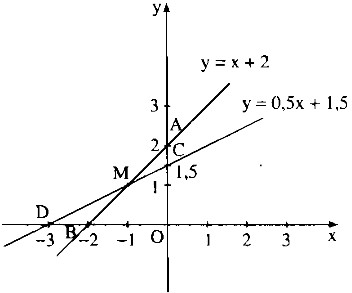
c) Khi a = 2 thì ta có hàm số: y = x + 2

Khi a = 1,5 thì ta có hàm số: y=0,5x+1,5y=0,5x+1,5

* Vẽ đồ thị của hàm số y=x+2y=x+2

Cho x = 0 thì y = 2. Ta có: A(0;2)

Cho y = 0 thì x = -2. Ta có: B(-2;0)

Đường thẳng AB là đồ thị hàm số y=x+2y=x+2.

* Vẽ đồ thị của hàm số y=0,5x+1,5y=0,5x+1,5

Cho x = 0 thì y = 1,5. Ta có: C(0;1,5)

Cho y = 0 thì x = -3. Ta có : B(-3;0)

Đường thẳng CD là đồ thị hàm số y=0,5x+1,5y=0,5x+1,5

* Tọa độ giao điểm  của hai đường thẳng .

Ta có: I thuộc đường thẳng y=x+2y=x+2 nên y1=x1+2y1=x1+2

            I thuộc đường thẳng y=0,5x+1,5y=0,5x+1,5 nên y1=0,5x1+1,5y1=0,5x1+1,5

Suy ra:

x1+2=0,5x1+1,5⇔0,5x1=–0,5⇔x1=–1x1+2=0,5x1+1,5⇔0,5x1=–0,5⇔x1=–1

x1=–1⇒y1=–1+2=1x1=–1⇒y1=–1+2=1           

Vậy tọa độ giao điểm của hai đường thẳng là I(-1;1).

a) Hàm số y = (m – 1)x + 3 là hàm số bậc nhất đối với x khi m – 1 ≠ 0 hay m ≠ 1 (*)

Hàm số đồng biến khi m – 1 > 0 hay m > 1.

Kết hợp với điều kiện (*) ta được với m > 1 thì hàm số đồng biến.

b) Hàm số y = (5 – k)x + 1 là hàm số bậc nhất đối với x khi 5 – k ≠ 0 hay k ≠ 5 (**).

Hàm số nghịch biến khi 5 – k < 0 hay k < 5.

Kết hợp với điều kiện (**) ta được với k < 5 thì hàm số nghịch biến.

a, y= 5x - (2-x)k = 5x - 2k + k.x = (5+k)x - 2k

Vậy hàm số có hệ số a= 5+k. Khi đó:

+ Hàm số đồng biến a > 0 ⇔ 5 + k > 0 ⇔ k > -5

+ Hàm số nghịch biến a < 0 ⇔ 5 + k < 0 ⇔ k < -5.

Hai đường thẳng y = ax + b và y = a'x + b' (a, a' ≠ 0)

   - Cắt nhau khi và chỉ khi a ≠ a'

   - Song song với nhau khi và chỉ khi a = a', b ≠ b'

   - Trùng nhau khi và chỉ khi a = a', b = b'

Đường thẳng song song Cho đường thẳng d có phương trình là y = a x + b ( a ≠ 0 ) y=ax+b(a≠0) và đường thẳng d' có phương trình là y = a ′ x + b ′ ( a ′ ≠ 0 ) y=a′x+b′(a′≠0). Khi đó d và d' song song khi và chỉ khi a = a ′ a=a′ và b ≠ b ′ b≠b′ Chú ý: nếu a=a' và b=b' thì d trùng d' 2. Đường thẳng cắt nhau Cho đường thẳng d có phương trình là y = a x + b ( a ≠ 0 ) y=ax+b(a≠0) và đường thẳng d' có phương trình là y = a ′ x + b ′ ( a ′ ≠ 0 ) y=a′x+b′(a′≠0). Khi đó d và d' cắt nhau khi và chỉ khi a ≠ a ′ a≠a′ Chú ý: nếu a ≠ a ′ a≠a′ và b=b' thì d cắt d' tại một điểm trên trục tung có tung độ là b

a) Hàm số đồng biến khi a > 0

b) Hàm số nghịch biến khi a < 0

Chúc bạn học tốt~

1. Định nghĩa

    Hàm số bậc nhất là hàm số có công thức: y=ax+by=ax+b trong đó aa và bb là các số đã cho với a≠0,xa≠0,x là biến số.

2. Sự biến thiên

    Hàm số bậc nhất y=ax+b(a≠0)y=ax+b(a≠0) có tập xác định D=RD=R, đồng biến trên RR nếu a>0a>0 và nghịch biến trên RR nếu a<0a<0.

15% à bn

mmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmmm