Bài 5. (1 điểm) Một khối đồ chơi gồm hai khối trụ $(H_1)$, $(H_2)$ xếp chồng lên nhau, lần lượt có bán kính đáy và chiều cao tương ứng là $r_1$ =, $h_1$, $r_2$, $h_2$ thỏa mãn $r_2 = \dfrac 12 r_1$, $h_2 = 2h_1$ (tham khảo hình vẽ).
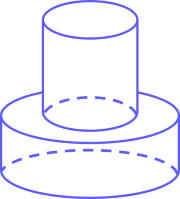
Biết rằng thể tích của toàn bộ khối đồ chơi bằng $30$ (cm3). Tính thể tích khối trụ $(H_1)$.
